数据结构基本查找算法


数据结构——基本查找算法
目录
前言
在程序的世界里,数据的价值在于被使用,而使用的第一步往往是“查找”。一个查找算法的选择,直接决定了程序的响应速度与资源消耗,尤其是在大数据时代,其影响更是天差地别。从O(n)到O(log n)的效率跃迁,背后是算法设计智慧的体现。
本文将聚焦于基本查找算法,深度剖析其内在原理与性能边界。我们将揭示:
- 顺序查找为何是通用性的代表,却又在效率上存在天花板。
- 二分查找如何通过“半区排除”策略,实现对数级的惊人效率,以及它必须遵守的“有序性”前提。
通过对比它们的时空复杂度、适用场景与实现细节,我们旨在为你建立一个清晰的决策框架,让你在纷繁复杂的实际问题中,能迅速选出最合适的那把“钥匙”。
一、 查找的概念
查找,又称搜索,是计算机科学中最基础、最核心的操作之一。它的定义非常直观:在一组数据集合中,找出满足特定条件的数据元素的过程。这个条件通常是数据元素的某个关键字(Key)与目标值相匹配。
小到在手机通讯录中搜索一个名字,大到互联网搜索引擎在海量网页中检索相关信息,其底层都依赖于高效的查找算法。
评判一个查找算法的优劣,主要取决于两大核心因素,它们共同决定了查找操作的效率:
- 数据本身的存储特性: 这是查找操作的“客观条件”。数据是有序还是无序?是存储在连续的内存空间(如数组)还是非连续的结构(如链表)?这些存储方式直接决定了我们可以采用哪种查找策略。
- 查找算法自身的特点: 这是查找操作的“主观策略”。算法是采用逐个比较的“线性”思路,还是能够跳跃式搜索的“分治”策略?算法本身的逻辑直接影响了其时间复杂度和空间复杂度。
二、经典查找算法
1.顺序查找
(1)算法说明
顺序查找,顾名思义,就是按照数据存储的自然顺序,从头到尾(或从尾到头)逐个进行比较,直到找到目标元素或遍历完整个数据集。
它通常被称为“线性查找”,因为其查找路径在逻辑上是一条直线。这是一种最朴素、最直观的查找方法,甚至可以说是一种“不是算法的算法”——因为它直接体现了解决问题最原始的思维。正因为如此,它也是在所有其他更高效的算法都不适用时,那个“最没办法的办法”。
时间复杂度:O(n)
- 在最坏情况下(目标元素在末尾或不存在),需要遍历整个包含
n个元素的集合。- 在平均情况下,也需要遍历大约一半的元素。
- 因此,顺序查找的时间复杂度为线性阶 O(n)。这意味着数据量增大一倍,最坏情况下的查找时间也大致会增加一倍。
(2)适用情况
数据存储无序
这是顺序查找最主要的应用场景。当数据集完全没有经过排序,无法利用“有序性”来跳过某些比较时,只能进行逐个比对。数据无法或不便于进行有效整理
- 数据结构限制: 对于某些线性结构,如单向链表,我们无法像数组那样通过下标进行随机访问。即使链表中的数据是有序的,也无法实现像二分查找那样的跳跃式访问,只能进行顺序遍历。
- 动态性极强: 如果数据集合更新极其频繁(频繁的插入和删除),维护其有序性的成本可能会高于顺序查找本身的成本。在这种情况下,直接进行顺序查找可能更实际。
- 数据量很小: 当数据量非常小的时候(例如,只有几个或几十个元素),各种高效算法带来的性能提升微乎其微,而顺序查找实现简单,反而更具优势。
(3)算法的优缺点:
优点:
- 算法简单,实现容易: 几行代码即可实现,不易出错。
- 通用性强: 对数据的存储结构没有任何额外要求,既适用于数组,也适用于链表。
- 无需预处理: 不需要数据事先有序,即来即用。
缺点:
效率低下:
当数据量
n很大时,O(n) 的时间复杂度使其性能成为瓶颈,不适合高性能要求的应用。
(4)示例代码
#include <stdio.h>
#include <math.h>
#include <time.h>
#include <stdlib.h>
#include <strings.h>
unsigned long long int count = 0;
#define DATA_NUM 1000*1000 // 内存元素个数
/**
* @brief 获取随机数据,并返回
* @note None
* @param range:控制获取的的随机数,至少是几位(个十百千万、十万、百万)
* @retval None
*/
int SEQ_SEARCH_Rand(int range)
{
return rand()%((int)pow(10, rand()%6+range+1));
}
/**
* @brief 查找数据
* @note None
* @param data_p:指向要查找的数据的内存的指针
* len: 内存元素的个数
* num: 要查找的数据
* @retval 成功:返回查找到的数据
* 失败:返回小于0的数据
*/
int SEQ_SEARCH_DataGet(unsigned int *data_p, unsigned int len, unsigned int num)
{
// 1、判断传进来的内存是否为空或者有没有数据
if ((data_p == NULL) || (len == 0))
return -1;
// 2、查找数据
for (int i = 0; i < len; i++)
{
// 计数执行了多少次
count++;
// 判断是否是找到的数据
if (data_p[i] == num)
{
printf("你要找的数据%d在第%d行!\n", data_p[i], i+1);
return data_p[i];
}
}
// 3、找不到数据,就返回-2
return -2;
}
/**
* @brief 将数据存储到txt文件中(数据太大,所以放文本里面,充当显示)
* @note None
* @param data_p:要写入数据的内存
* file: 要读取数据的文件
* @retval None
*/
int SEQ_SEARCH_StoreData(unsigned int *data_p, const char *file)
{
FILE *fp = fopen(file, "w"); // 1、创建并打开文件(以写权限打开),并返回一个文件流控制符
for (int i = 0; i < DATA_NUM; i++) // 2、将海量数据写入到文本中
{
fprintf(fp, "%06d = %u\n", i, data_p[i]);
}
fclose(fp); // 3、关闭文件
}
// 主函数
int main(int argc, char const *argv[])
{
// (1)、产生无序数据,并赋值给相应的内存空间
// 1、使用时间作为随机数的变化量
srand(time(NULL));
// 2、申请堆空间,用来存放数据 --- PS:栈空间=8M, 堆空间:几个G(看你的电脑的硬盘和系统支持度)
unsigned int *data_p = malloc(sizeof(unsigned int)*DATA_NUM);
bzero(data_p, sizeof(unsigned int)*DATA_NUM);
// 3、存放数据
for (unsigned int i = 0; i < DATA_NUM ; i++)
{
*(data_p+i) = SEQ_SEARCH_Rand(1);
}
// (2)、将数据加载到.txt文件中
SEQ_SEARCH_StoreData(data_p, "./顺序查找文本.txt"); // 这里只做显示使用(通常来讲,是读取文件数据到堆空间,然后再处理数据的)
// (3)、查找数据
int check_num = 0;
while (1)
{
// 1、输入要查找的数据
printf("请输入你要找的数据(正整数):\n");
scanf("%d", &check_num);
// 2、返回找的数据
int ret = SEQ_SEARCH_DataGet(data_p, DATA_NUM, check_num);
if (ret == -1)
{
printf("data_p指向的内存的数据为空的\n");
}
else if(ret == -2)
{
printf("没有在data_p指向的内存中找到数据!\n");
}
printf("一共找了%llu次!\n", count);
count = 0;
}
return 0;
}2.分块查找
(1)算法说明
分块查找,又称索引顺序查找,它实质上是一种通过建立索引来优化查找过程的算法。它将查找过程清晰地分为两个步骤:
在索引中确定块:
- 将整个数据集分成若干个子集,称为“块”。
- 为每一块建立一个索引项,索引项通常包含该块中数据的最大关键字(或最小关键字)以及该块的起始地址。
- 查找时,首先在索引表中进行查找,确定目标数据可能存在于哪一块中。因为索引表是有序的,所以这一步可以使用高效的查找算法(如二分查找)。
在确定的块内进行查找:
- 根据索引项提供的地址,找到对应的数据块。
- 然后在该数据块内进行查找。由于块内的数据可以是无序的,因此这一步通常采用顺序查找。
(2)举例说明
假设有一个数组 [22, 12, 9, 33, 42, 48, 60, 55, 70, 65, 88, 80],我们将其分为3块。
- 块1:
[22, 12, 9, 33]-> 最大关键字:33 - 块2:
[42, 48, 60, 55]-> 最大关键字:60 - 块3:
[70, 65, 88, 80]-> 最大关键字:88
建立索引表: 索引表是一个有序表,记录了每块的最大关键字和起始地址。
| 最大关键字 | 起始地址 |
|---|---|
| 33 | 0 |
| 60 | 4 |
| 88 | 8 |
查找:
- 索引查找: 在索引表中查找 48。因为 33 < 48 <= 60,所以确定 48 在第二块。
- 块内查找: 根据索引表,找到第二块的起始地址是 4,然后在该块
[42, 48, 60, 55]内进行顺序查找,成功找到 48。
(3)性能分析与特点
时间复杂度:
分块查找的性能介于顺序查找和二分查找之间。假设有
n个数据,平均分成b块,每块有s个元素(n = b * s)。
- 索引查找的平均时间复杂度为 O(log b) 或 O(b)(取决于索引查找算法)。
- 块内查找的平均时间复杂度为 O(s)。
- 总的时间复杂度约为 O(log b + s)。当块数
b和块内元素数s接近 √n 时,性能较优。
适用条件:
- 数据集合庞大,且难以整体排序,但可以分块。
- 块内数据可以无序,但块与块之间必须有序(即后一块的所有关键字必须大于前一块的最大关键字)。
- 非常适合数据库索引、文件系统等外部存储查找场景。
(4)示例代码
#include <stdio.h>
#include <math.h>
#include <time.h>
#include <stdlib.h>
#include <strings.h>
#include <string.h>
#include <stdbool.h>
unsigned long long int count = 0;
#define STRING_MAX_LEN 20 // 字符串的最大长度
#define DATA_NUM 1000*1000 // 内存元素个数
/**
* @brief 生成随机字符数组(1)
* @note None
* @param None
* @retval 成功:返回随机字符数组
* 失败:NULL
*/
char* BLOCK_SEARCH_Rand(void)
{
int len = rand()%(STRING_MAX_LEN); // 规定字符串的最长的长度为STRING_MAX_LEN
len = ((len<2)?2:len); // 规定字符串的最短的长度为2
char* s =calloc(1, len); // 申请len个字节的堆空间
if (s==NULL)
return NULL;
char letter[] = {'a', 'A'}; // 随机你的字符为小写a还是大写A
for (int i = 0; i < len; i++)
s[i] = letter[rand()%2] + rand()%26;
// 随机你的字符为小写a还是大写A,再在此基础上
// 加0到25的数据,从而形成a到z,A到Z的随机字母
// 返回生成的随机字符数组
return s;
}
/**
* @brief 将数据存储到txt文件中
* @note None
* @param data_p:二维数组(里面的每一个一维数组,都是字符数组)
* file: 要读取数据的文件
* @retval None
*/
int BLOCK_SEARCH_StoreData(char data_p[][STRING_MAX_LEN], const char *file)
{
FILE *fp = fopen(file, "w"); // 1、创建并打开文件(以写权限打开),并返回一个文件流控制符
for (int i = 0; i < DATA_NUM; i++) // 2、将海量数据写入到文本中
{
fprintf(fp, "%06d = %s\n", i, data_p[i]);
}
fclose(fp); // 3、关闭文件
}
/**
* @brief 在索引(目录)中找到数据所属分块
* @note 根据字符串开头字符的大小写来寻找
* @param data_p:二维数组(里面的每一个一维数组,都是字符数组)
* index: 二级指针(里面的每一个一级指针,都指向了一个字符数组)
* @retval None
*/
void BLOCK_SEARCH_CreateIndex(char data_p[][STRING_MAX_LEN], int **index )
{
// 1、统计各个首字符出现的频次
int n[52] = {0}; // ['a'...'z'和'A'...'Z'共:52个]
for (int i = 0; i < DATA_NUM; i++) // 在所有数据中找每一行字符串的首字符
{ // b E
int pos = (data_p[i][0]>='a')?(data_p[i][0]-'a'):(data_p[i][0]-'A'+26);
/*
说明:
找到的首字符的ASCII值,其值大于'a',则为小写(算出其位置)
其值小于'a',则为大写(算出其位置)
*/
n[pos]++; // 统计各个首字符出现的频次
}
// 2、给index分配内存
for (int i = 0; i < 52; i++)
{
index[i] = calloc(1+n[i], sizeof(int));
}
// 3、记录每个字符出现的行号
for (int i = 0; i < DATA_NUM; i++)
{
int pos = (data_p[i][0]>='a')?(data_p[i][0]-'a'):(data_p[i][0]-'A'+26); // 记录输入的字符串的首个字符是52个大小写字母数组中的第几个位置
int j = ++index[pos][0]; // 在分块好的块中排第几个
index[pos][j] = i; // 总行数赋值给对应字符串的行数
}
}
// 主函数
int main(int argc, char const *argv[])
{
// (1)、产生无序数据(字符串),并赋值给相应的内存空间
// 1、使用时间作为随机数的变化量
srand(time(NULL));
// 2、申请堆空间,用来存放数据 --- PS:栈空间=8M, 堆空间:几个G(看你的电脑的硬盘和系统支持度)
char (*data_p)[STRING_MAX_LEN] = calloc(DATA_NUM, STRING_MAX_LEN);
// 3、存放数据
for (unsigned int i = 0; i < DATA_NUM ; i++)
{
char *s = BLOCK_SEARCH_Rand();
strncpy(data_p[i], s, strlen(s));
free(s);
}
// (2)、再将数据加载到.txt文件中
BLOCK_SEARCH_StoreData(data_p, "./分块查找文本.txt");
// (3)、利用索引,进行查找
char str[32] = {0};
printf("请输入你要查找的字符串:\n");
int **index = calloc(52, sizeof(int*));
BLOCK_SEARCH_CreateIndex(data_p, index);
while(1)
{
// 从键盘接收一个待查的字符串,并去掉回车符
bzero(str, 32);
fgets(str, 32, stdin);
strtok(str, "\n");
bool done = false;
for (int i = 1; i < DATA_NUM; i++)
{
count++;
// 小写字母[00到25],大写字母[26到51]
int pos = (str[0]>='a')?(str[0]-'a'):(str[0]-'A'+26);
if ( (i<=index[pos][0]) && (strcmp(data_p[index[pos][i]], str)==0) )
{
printf("你要找的字符串在第%d行!\n", index[pos][i]);
done = true;
break;
}
else if(i>index[pos][0])
break;
}
if(!done)
printf("没有你要找的字符串!\n");
printf("一共找了%llu次!\n", count);
count = 0;
}
return 0;
}3.二分查找
(1)算法说明
二分查找算法是计算机科学中最优美且高效的算法之一。它有一个重要的前提条件:待查找的数据集必须是有序的(无论是升序还是降序)。
这个条件意味着,如果数据本身是无序的,我们需要在查找前对其进行一次排序。虽然排序本身有成本,但如果数据量较大且在一段时间内相对稳定,不会发生大面积更新,那么一次排序的开销可以被后续大量高效的查找操作所分摊,从而带来整体性能的显著提升。在这种情况下,使用二分查找是极佳的选择。
时间复杂度:
二分查找每次比较都能将搜索范围缩小一半,这是一种指数级的缩减速度。因此,即使面对海量数据,它也能在极少的步骤内完成查找,其时间复杂度为对数阶 O(log n),效率远高于顺序查找的 O(n)。
(2)算法的核心思路
二分查找的核心思想是 “分而治之” 。它通过不断将有序数据集对半分割,并通过中间元素与目标值的比较来排除一半的搜索空间,从而快速定位目标。
具体步骤(以升序数组为例):
初始化边界: 设定两个指针,
low指向搜索区间的起始位置,high指向搜索区间的末尾位置。循环条件: 只要
low指针没有超过high指针(即low <= high),就继续执行步骤3-5。计算中间点: 取当前搜索区间
[low, high]的中间位置mid。通常使用mid = low + (high - low) / 2来计算,这样可以有效防止整数溢出。比较与判断:
- 如果
array[mid]等于目标值,查找成功,返回mid。- 如果
array[mid]小于目标值,说明目标值只可能存在于右半部分。调整low指针为mid + 1,在右半区间继续查找。- 如果
array[mid]大于目标值,说明目标值只可能存在于左半部分。调整high指针为mid - 1,在左半区间继续查找。重复: 回到步骤2,在新的搜索区间内继续执行。
查找失败: 如果循环结束仍未找到目标值,则查找失败。
简单来说: “从中间开始找,比较一次就能排除一半的数据。再在剩下的一半里重复这个过程,直到找到目标或确定目标不存在。”
(3)算法解释
假设我们有如图所示的数组:
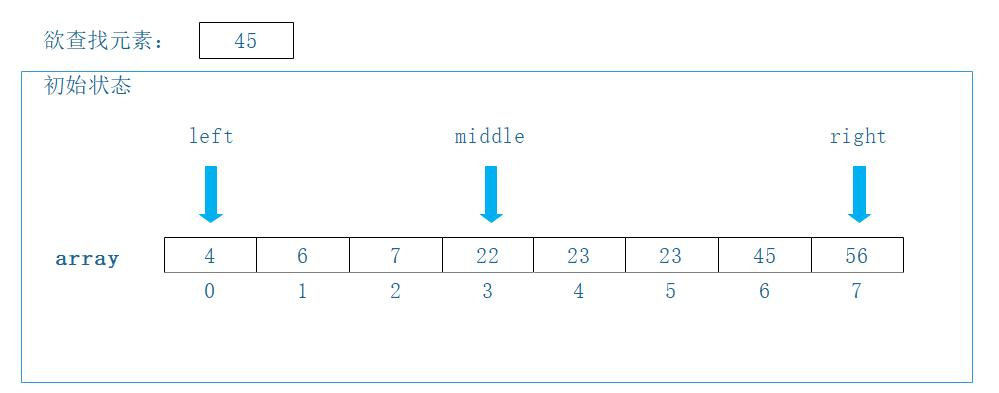
现在想要在此有序数组(从小到大)的数据中,查找45:
- left 指针指向索引 0(元素 4)。
- right 指针指向索引 7(元素 56)。
- middle 指针通过计算得出,指向索引 3(元素 22)。计算方式为:
middle = (left + right) / 2 = (0 + 7) / 2 = 3(向下取整)。
第一步:比较与决策
- 将中间元素
array[middle](即22)与目标值45进行比较。- 比较结果:
22 < 45。- 逻辑判断: 由于数组是升序的,且中间值小于目标值,这意味着目标值
45只可能存在于当前中间点的右侧区域。- 操作: 将 left 指针移动到 middle + 1 的位置,即索引 4(元素 23)。这样,搜索范围被缩小为右半部分:
[23, 23, 45, 56](索引 4 到 7)。第二步:在新的范围内继续查找
- 新的搜索区间:
left = 4,right = 7。- 计算新的 middle 索引:
(4 + 7) / 2 = 5(向下取整)。- 此时
middle指向索引 5,对应的元素是23。- 比较结果:
23 < 45。- 逻辑判断: 目标值仍然在右侧。
- 操作: 再次将 left 指针移动到 middle + 1 的位置,即索引 6(元素 45)。搜索范围进一步缩小为
[45, 56](索引 6 到 7)。第三步:找到目标
- 新的搜索区间:
left = 6,right = 7。- 计算新的 middle 索引:
(6 + 7) / 2 = 6(向下取整)。- 此时
middle指向索引 6,对应的元素是45。- 比较结果:
45 == 45。- 结论: 查找成功!目标值
45在数组中的索引位置为 6。
| 步骤 | left | right | middle | array[middle] | 比较结果 | 操作 |
|---|---|---|---|---|---|---|
| 初始 | 0 | 7 | 3 | 22 | 22 < 45 | 搜索右半部分,left = 4 |
| 第1次 | 4 | 7 | 5 | 23 | 23 < 45 | 搜索右半部分,left = 6 |
| 第2次 | 6 | 7 | 6 | 45 | 45 == 45 | 查找成功,返回索引 6 |
(4)算法的优缺点
优点:
- 效率极高: O(log n) 的时间复杂度使其在处理大规模有序数据时优势巨大。
缺点:
- 依赖有序数据: 前提条件苛刻,必须保证数据集有序。
- 仅适用于顺序存储结构: 依赖下标随机访问,因此适用于数组,但不适用于链表等非随机访问的数据结构。
稳定性:
二分查找本身是查找算法,不涉及数据移动,故无稳定性问题。
(5)示例代码
#include <stdio.h>
#include <math.h>
#include <time.h>
#include <stdlib.h>
#include <strings.h>
unsigned long long int count = 0;
#define DATA_NUM 1000*1000 // 内存元素个数
/**
* @brief 获取随机数据,并返回
* @note None
* @param range:控制获取的的随机数,至少是几位(个十百千万、十万、百万)
* @retval None
*/
int BIN_SEARCH_Rand(int range)
{
return rand()%((int)pow(10, rand()%6+range+1));
}
/**
* @brief 查找数据
* @note 二分查找法
* @param data_p:指向要查找的数据的内存的指针
* len: 内存元素的个数
* num: 要查找的数据
* @retval 成功:返回查找到的数据
* 失败:返回小于0的数据
*/
int BIN_SEARCH_DataGet(unsigned int *data_p, unsigned int len, unsigned int num)
{
// 1、判断传进来的内存是否为空或者有没有数据
if ((data_p == NULL) || (len == 0))
return -1;
// 2、查找数据
int left = 0;
int right = len-1;
int middle = 0;
while (left<=right) // 二分法的极限,已经将所有的数据比较完
{
count++; // 记录查询了几次
middle = (left+right)/2; // 获取中间的位置
if (num == data_p[middle]) // 判断是否找到了数据,并返回该值的行数和值
{
printf("你要找的数据在第%d行", middle);
return data_p[middle];
}
if (num < data_p[middle]) // num小于中间值,则其右边的所有数据包括原先的中间值都可以不用计算
right = middle-1;
else // num大于中间值,则其左边的所有数据包括原先的中间值都可以不用计算
left = middle+1;
}
// 3、找不到数据
return -2;
}
/**
* @brief 将数据存储到txt文件中(数据太大,所以放文本里面,充当显示)
* @note None
* @param data_p:要写入数据的内存
* file: 要读取数据的文件
* @retval None
*/
int BIN_SEARCH_StoreData(unsigned int *data_p, const char *file)
{
FILE *fp = fopen(file, "w"); // 1、创建并打开文件(以写权限打开),并返回一个文件流控制符
for (int i = 0; i < DATA_NUM; i++) // 2、将海量数据写入到文本中
{
fprintf(fp, "%06d = %u\n", i, data_p[i]);
}
fclose(fp); // 3、关闭文件
}
/**
* @brief 交换两个数据
* @note None
* @param num1:指向要交换的整型数据1的指针
* num2:指向要交换的整型数据2的指针
* @retval None
*/
void __Swap(unsigned int *num1, unsigned int *num2)
{
unsigned int tmp = 0; // 交换两个数据的中间值
tmp = *num1; // 交换两个数据的值
*num1 = *num2;
*num2 = tmp;
}
/**
* @brief 快速排序
* @note None
* @param data_p: 指向要排序数据内存的指针
* len: 数据内存的长度
* @retval 成功:返回0
* 失败:返回-1
*/
int QUICK_SORT_DataSort(unsigned int *data_p, unsigned int len)
{
// 10
// 1、退出条件
if (len <= 1)
return 0;
// 2、
int i = 0; // 0
int j = len-1; // 不断递进的过程 // 9
while (i<j)
{
// 从右到左比较,顺序j--, 逆序交换
while ( (data_p[i] <= data_p[j]) && (i<j))
{
j--;
}
__Swap(&data_p[i], &data_p[j]);
// 从左到右比较,顺序i++,逆序交换
while ( (data_p[i] <= data_p[j]) && (i<j))
{
i++;
}
__Swap(&data_p[i], &data_p[j]);
}
// 3、不断逼近结果
QUICK_SORT_DataSort(data_p, i); // 解决左边序
QUICK_SORT_DataSort(data_p+i+1, len-i-1); // 解决右边序
}
// 主函数
int main(int argc, char const *argv[])
{
// (1)、产生无序数据,并赋值给相应的内存空间
// 1、使用时间作为随机数的变化量
srand(time(NULL));
// 2、申请堆空间,用来存放数据 --- PS:栈空间=8M, 堆空间:几个G(看你的电脑的硬盘和系统支持度)
unsigned int *data_p = malloc(sizeof(unsigned int)*DATA_NUM);
bzero(data_p, sizeof(unsigned int)*DATA_NUM);
// 3、存放数据
for (unsigned int i = 0; i < DATA_NUM ; i++)
{
*(data_p+i) = BIN_SEARCH_Rand(1);
}
// (2)、先排序,再将数据加载到.txt文件中
QUICK_SORT_DataSort(data_p, DATA_NUM);
BIN_SEARCH_StoreData(data_p, "./二分查找文本.txt"); // 这里只做显示使用(通常来讲,是读取文件数据到堆空间,然后再处理数据的)
// (3)、查找数据
int check_num = 0;
while (1)
{
// 1、输入要查找的数据
printf("请输入你要找的数据(正整数):\n");
scanf("%d", &check_num);
// 2、返回找的数据
int ret = BIN_SEARCH_DataGet(data_p, DATA_NUM, check_num);
if (ret == -1)
{
printf("data_p指向的内存的数据为空的\n");
}
else if(ret == -2)
{
printf("没有在data_p指向的内存中找到数据!\n");
}
printf("一共找了%llu次!\n", count);
count = 0;
}
return ;
}