算法日记-新动计划

JAY.LIN 收录于未分类

2025-09-21 约 1507 字预计阅读 4 分钟

https://bing.ee123.net/img/rand?artid=151785606

算法日记—新动计划

前言

LeetCode【新】动计划提单用于巩固基础语法，是新手小白入门的首选，此篇对一些题目进行解析和记录。

一、

给你一个字符串 s ，将该字符串中的大写字母转换成相同的小写字母，返回新的字符串。

本题重点在于如何将大写字母转换为小写字母：将大写字母的ASCII码加上小写字母和对应大写字母在ASCII码上的差值（32）即获得小写字母

1.创建StringBuilder对象result，用于高效拼接字符串的类，若使用普通的String进行拼接，每次拼接都会生成一个新的String对象，效率较低，而StringBuilder可以在原有对象基础上进行修改，提高效率。

2.for(char c:s.toCharArray())使用增强for循环遍历字符串s转换为字符数组后的每个字符，s.toCharArray()方法将字符串s转换为一个字符数组，这样就可以逐个获取字符串中的字符了。

4.将处理后的字符c无论是原本的小写字母、非字母字符还是转换后的小写字母。全部通过append方法添加到StringBuilder对象result中

5.将StringBuilder对象result转换为String类型并返回。

class Solution {
    public String toLowerCase(String s) {
        StringBuilder result=new StringBuilder();
        for(char c:s.toCharArray()){
            if (c >= 'A' && c <= 'Z') {
                c = (char) (c + ('a' - 'A'));
        }
        result.append(c);
    }
    return result.toString();
}
}

二、

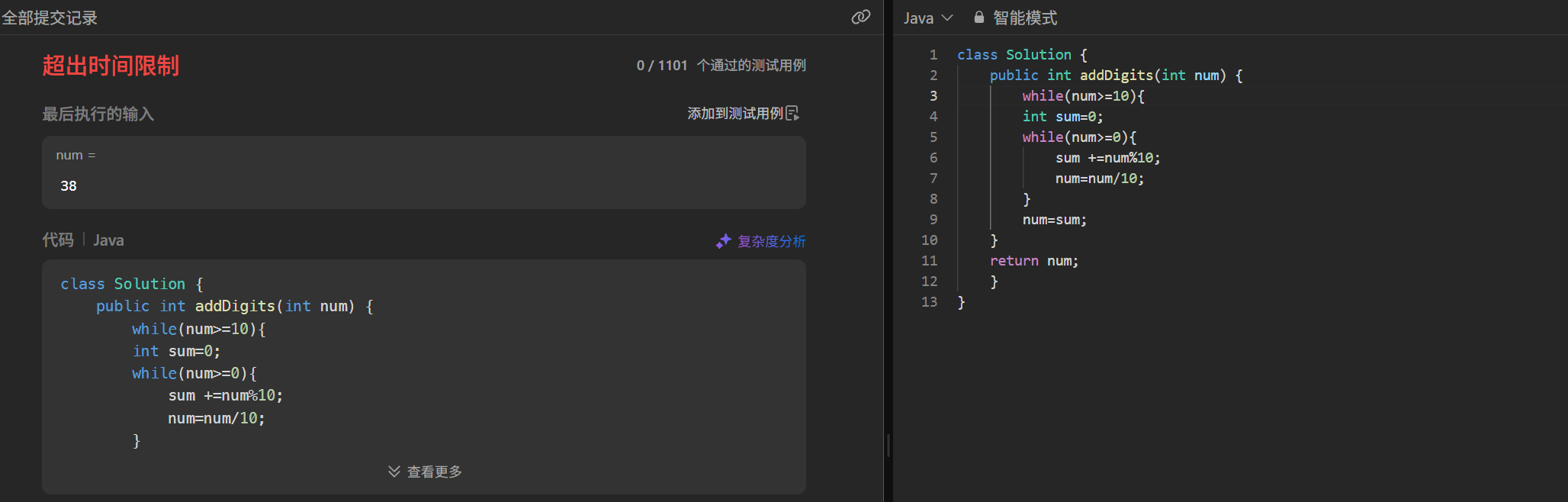
1.第一种方法：模拟各位相加的过程：超时

外层 while 循环判断 num 是否大于等于 10，如果是，说明还需要继续各位相加。
内层 while 循环用于计算当前 num 各位数字的和，通过取余（num % 10）得到个位数字，累加到 sum 中，然后通过整除（num /= 10）去掉个位数字，直到 num 变为 0。
最后将 sum 赋值给 num，继续外层循环判断，直到 num 是一位数，返回 num。

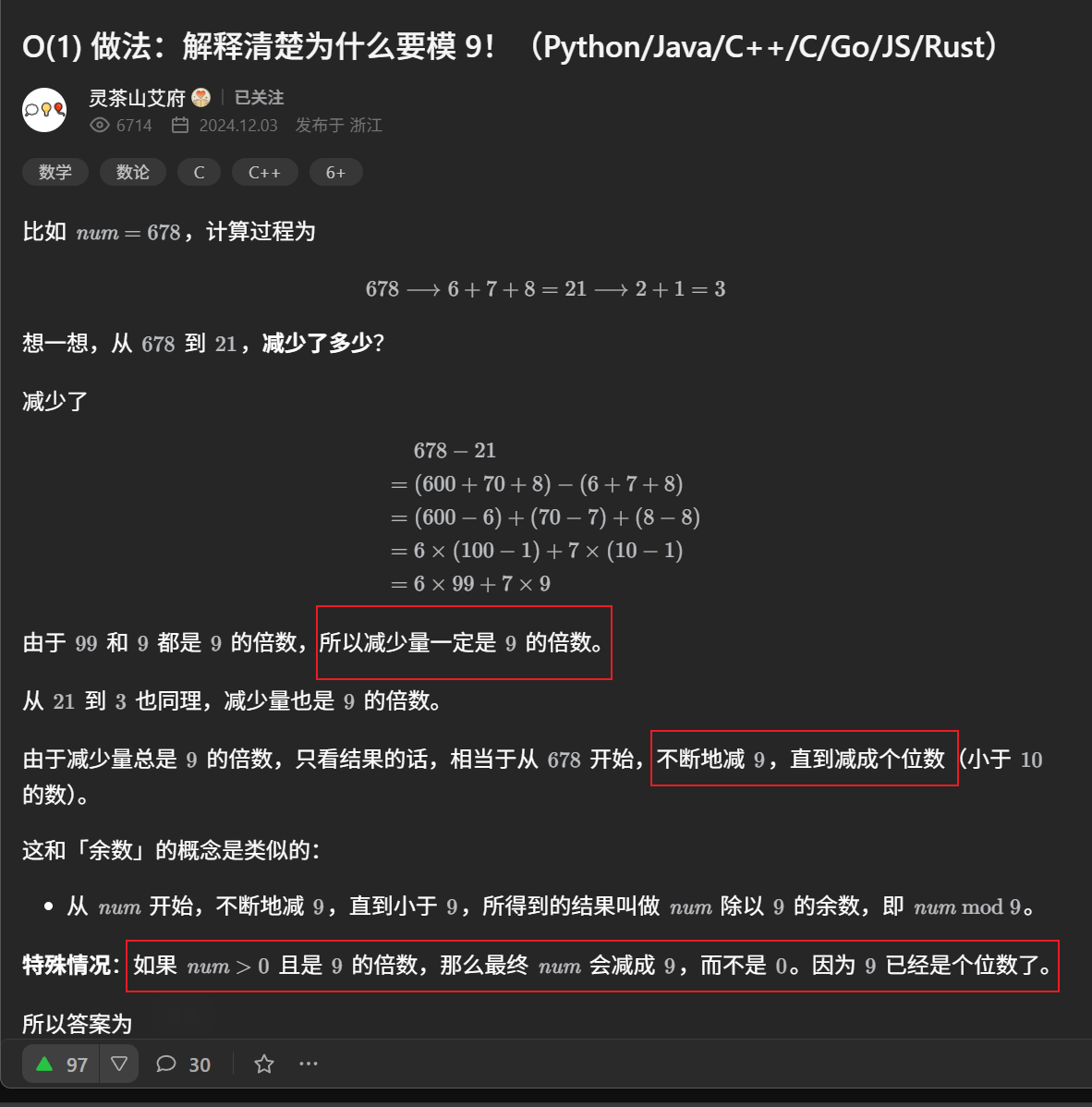
**进阶：**你可以不使用循环或者递归，在 O(1) 时间复杂度内解决这个问题吗？

以下为灵神的题解

class Solution {
    public int addDigits(int num) {
        return (num - 1) % 9 + 1;
    }
}

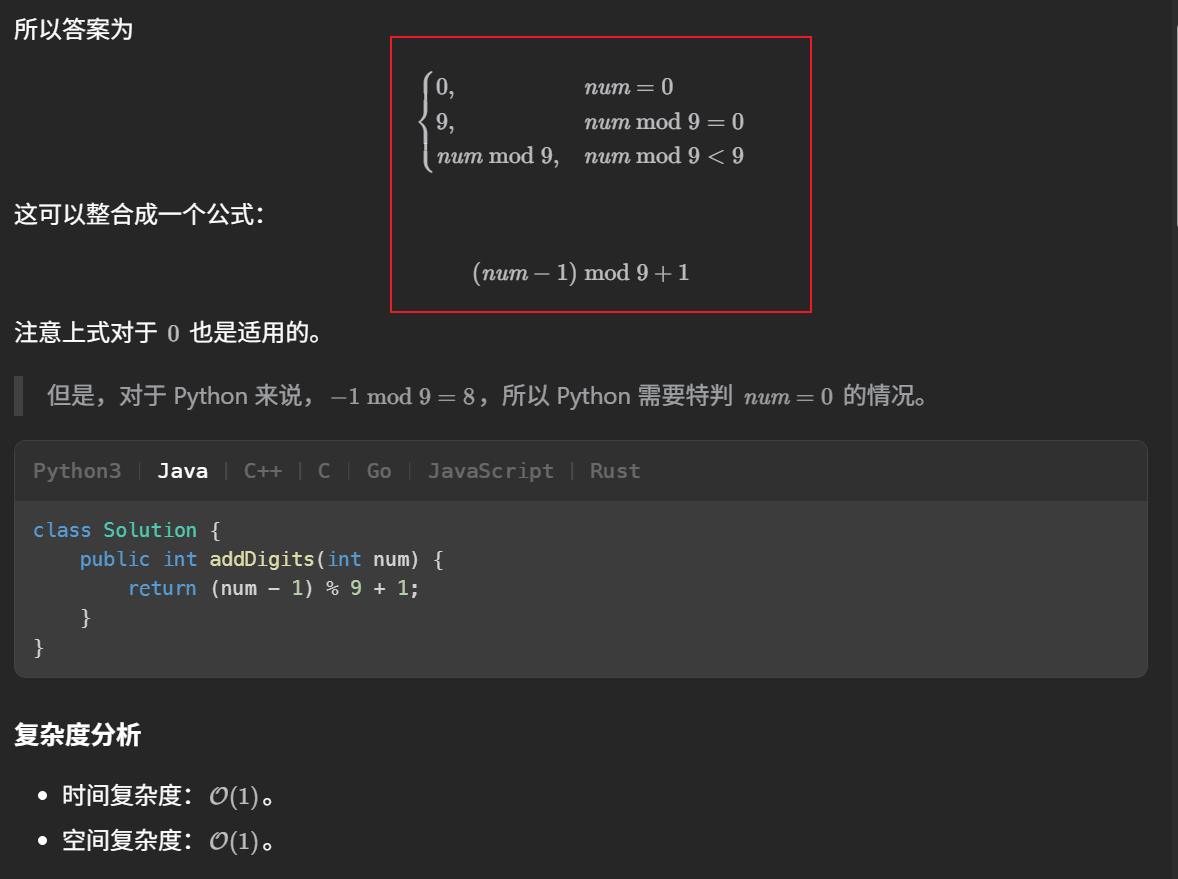
如果无法总结出公式，进行if判断，结果也是一样的。

class Solution {
    public int addDigits(int num) {
        if (num == 0) {
            return 0;
        }
        int remainder = num % 9;
        return remainder == 0 ? 9 : remainder;
    }
}

三、

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

以下是使用位运算进行解答，时间复杂度O(1)

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n>0 && (n&(n-1))==0;
    }
}

当然也可以使用循环或递归，时间复杂度为O(log n)

class Solution {
    public boolean isPowerOfTwo(int n) {
        if (n <= 0) return false;
        while (n % 2 == 0) {
            n /= 2;
        }
        return n == 1;
    }
}

class Solution {
    public boolean isPowerOfTwo(int n) {
        if (n <= 0) return false;
        if (n == 1) return true;
        if (n % 2 != 0) return false;
        return isPowerOfTwo(n / 2);
    }
}

通过递归逐步将数字减半，检查最终是否能得到 1。

更多位运算技巧，可参考灵神的《》

四、

class Solution {
    public int[][] transpose(int[][] matrix) {
        int n=matrix.length;
        int m=matrix[0].length;
        int[][] ans=new int[m][n];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                ans[j][i]=matrix[i][j];
            }
        }
        return ans;
    }
}

五、

class Solution {
    public int[] shuffle(int[] nums, int n) {
        int[] ans=new int[2*n];
        for(int i=0;i<n;i++){
            ans[2*i]=nums[i];
            ans[2*i+1]=nums[i+n];
        }
        return ans;
    }
}

六、

class Solution {
    public int maxScore(String s) {
        int ans=0;
        int n=s.length();
        for(int i=1;i<n;i++){
            int score=0;
            for(int j=0;j<i;j++){
            if(s.charAt(j)=='0'){
                score++;
            }
            }
            for(int j=i;j<n;j++){
                if(s.charAt(j)=='1'){
                    score++;
                }
            }
            ans=Math.max(ans,score);
        }
        return ans;
    }
}

七、

这题依旧是二分，虽然有点不一样但本质还是不断缩小二分的范围，最后确定，那么缩小的条件是什么呢？—arr[mid]>arr[mid+1]

我们的目标是通过二分查找，找到第一个满足 arr[mid] > arr[mid+1] 的位置（因为从该位置开始，数组进入「递减段」，而它本身就是峰值）。

二分过程中，left 和 right 的移动规则是：

如果 arr[mid] > arr[mid+1]：说明 mid 可能在「递减段」，峰值可能在 mid 或 mid 左侧，因此调整 right = mid - 1，尝试在左半段继续查找。
如果 arr[mid] <= arr[mid+1]：说明 mid 在「递增段」，峰值一定在 mid 右侧，因此调整 left = mid + 1，去右半段查找。

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        //因为答案一定在[1,n-2]中，所以初始化如下
        int left=1;
        int right=arr.length-2;
        while(left<=right){
            int mid=(left+right)>>>1;
            if(arr[mid]>arr[mid+1]){
                //二分右边界时，一定成立
                right=mid-1;
            }
            else{
                //二分左边界时，一定不成立
                left=mid+1;
            }
        }
                // 循环结束后，left 就是峰值元素的下标
        return left;
    }
}

总结

加油

目录

算法日记-新动计划

算法日记—新动计划

前言

一、

二、

三、

四、

五、

六、

七、

总结