算法基础篇3高精度

目录

算法基础篇(3)高精度
当数据的值特别大,各种类型都存不下的时候,此时就需要用高精度算法来计算加减乘除。先用字符串读入这个数,然后用数组逆序存储该数的每一位;利用数组,模拟加减乘除运算的过程。高精度算法本质上还是模拟算法,用代码模拟小学列竖式计算加减乘除的过程。
一、高精度加法
算法原理:模拟小学列竖式计算的过程
1、先用字符串读入,拆分每一位,逆序放在数组中
2、利用数组,模拟小学列竖式计算加法的过程
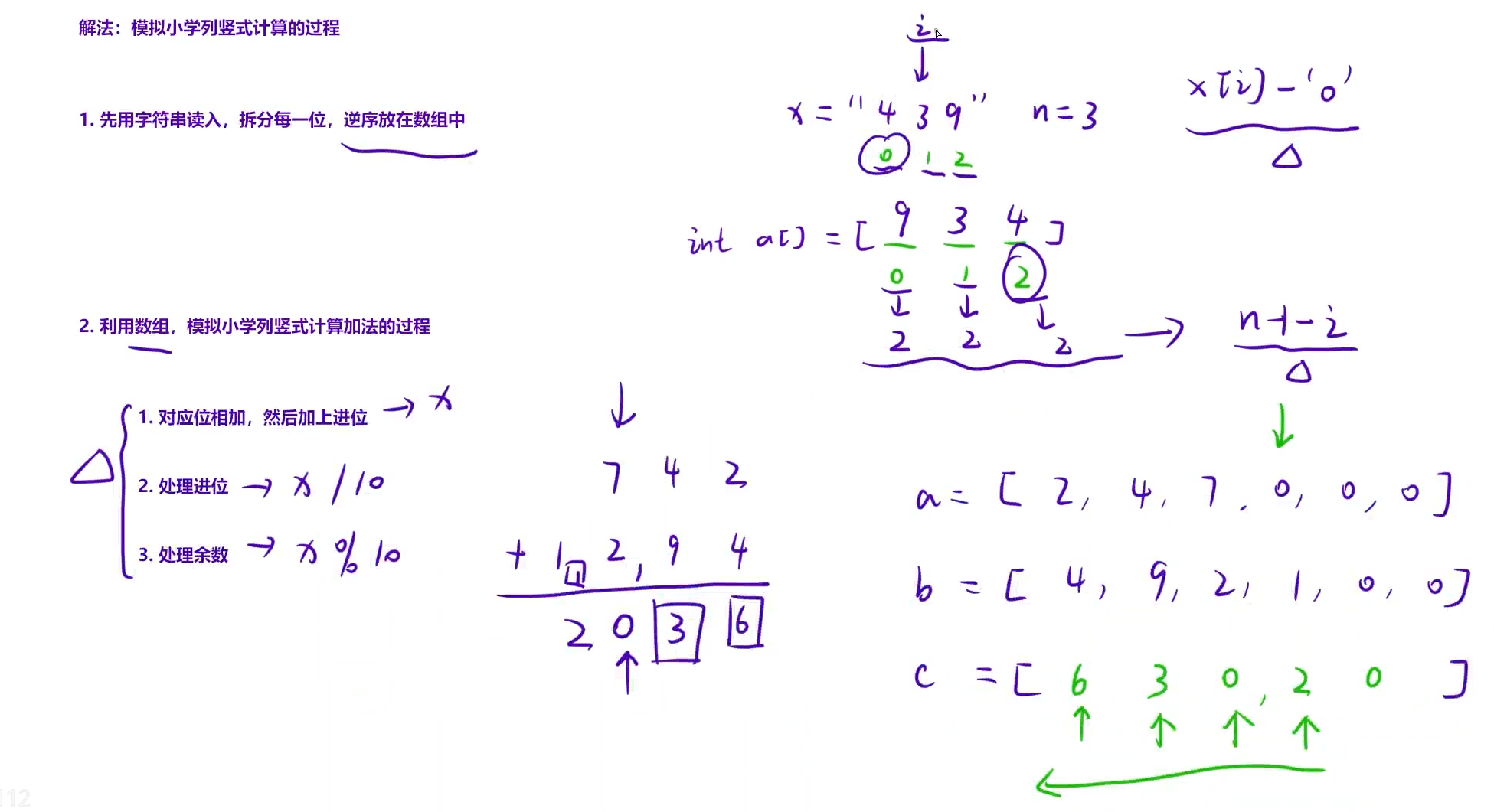
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
size_t la, lb, lc;
// 高精度加法的模版 --- c = a + b
void add(int c[], int a[], int b[])
{
for (int i = 0;i < lc;i++)
{
c[i] += a[i] + b[i]; //对应位相加,再加上进位
c[i + 1] += c[i] / 10; //处理进位
c[i] %= 10; //处理余数
}
if (c[lc])
{
lc++;
}
}
int main()
{
string x, y;
cin >> x >> y;
//1.拆分每一位,逆序放在数组中
la = x.size();
lb = y.size();
lc = max(la, lb);
for (int i = 0;i < la;i++)
{
a[la - 1 - i] = x[i] - '0';
}
for (int i = 0;i < lb;i++)
{
b[lb - 1 - i] = y[i] - '0';
}
//2.模拟加法的过程
add(c, a, b); // c = a + b
//输出结果
for (int i = lc - 1;i >= 0;i--)
{
cout << c[i];
}
return 0;
}二、高精度减法
算法思路:模拟列竖式计算的过程
先比较大小,然后用较大数减去较小数。如果直接用字符串来比较大小,是会出错的(比如:数字:101 > 99,但是字符串"101" < “99”)。用字符串比较之前,要先比较一下长度。

参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
//比大小
bool cmp(string& x, string& y)
{
//先比较长度
if (x.size() != y.size())
return x.size() < y.size();
//再按照字典序的方式比较
return x < y;
}
//高精度减法的模板 --- c = a - b
void sub(int c[], int a[], int b[])
{
for (int i = 0;i < lc;i++)
{
c[i] += a[i] - b[i]; //对应位相减,然后处理借位
if (c[i] < 0)
{
c[i + 1] -= 1; //借位
c[i] += 10;
}
}
//处理前导零
while (lc > 1 && c[lc - 1] == 0)
{
lc--;
}
}
int main()
{
string x, y;
cin >> x >> y;
//比大小
if (cmp(x, y))
{
swap(x, y);
cout << '-';
}
//1.拆分每一位,然后逆序放在数组中
la = x.size();
lb = y.size();
lc = max(la, lb);
for (int i = 0;i < la;i++)
{
a[la - 1 - i] = x[i] - '0';
}
for (int i = 0;i < lb;i++)
{
b[lb - 1 - i] = y[i] - '0';
}
//2.模拟减法的过程
sub(c, a, b); //c = a - b
//输出结果
for (int i = lc - 1;i >= 0;i--)
{
cout << c[i];
}
return 0;
}三、高精度乘法
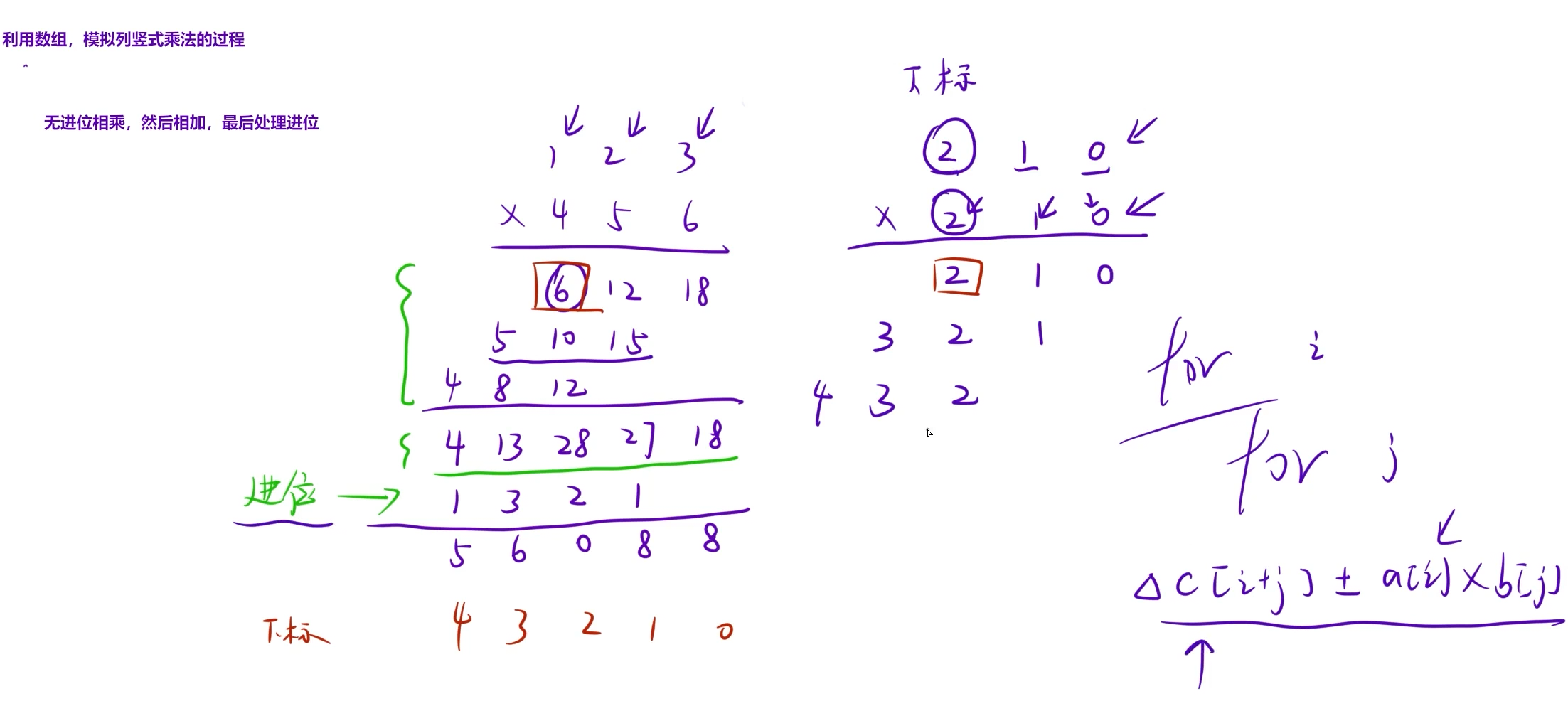
算法思路:模拟列竖式计算的过程
先用字符串读入,然后拆分每一位,逆序放在数组中。利用数组,模拟列竖式乘法的过程。
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
//高精度乘法的模板 --- c = a * b
void mul(int c[], int a[], int b[])
{
//无进位相乘,然后相加
for (int i = 0;i < la;i++)
{
for (int j = 0;j < lb;j++)
{
c[i + j] += a[i] * b[j];
}
}
//处理进位
for (int i = 0;i < lc;i++)
{
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
//处理前导零
while (lc > 1 && c[lc - 1] == 0)
{
lc--;
}
}
int main()
{
string x, y;
cin >> x >> y;
//1.拆分每一位,逆序放在数组中
la = x.size();
lb = y.size();
lc = la + lb;
for (int i = 0;i < la;i++)
{
a[la - 1 - i] = x[i] - '0';
}
for (int i = 0;i < lb;i++)
{
b[lb - 1 - i] = y[i] - '0';
}
//2.模拟乘法的过程
mul(c, a, b); //c = a * b
//输出结果
for (int i = lc - 1;i >= 0;i--)
{
cout << c[i];
}
return 0;
}四、高精度除法
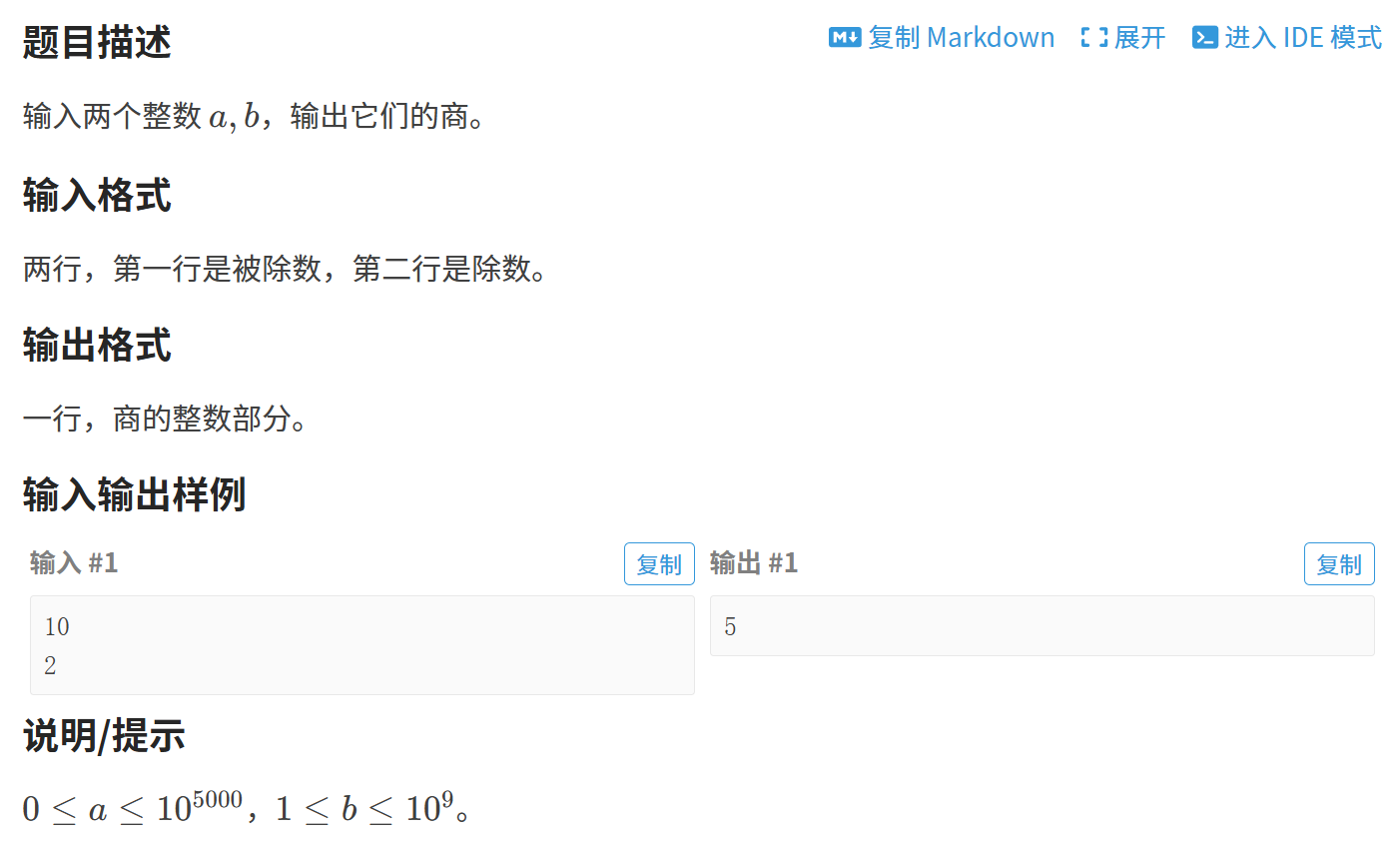
算法思路:模拟列竖式计算的过程
用字符串读入第一个数,拆分每一位,逆序放在数组中。利用数组,模拟列竖式除法的过程。
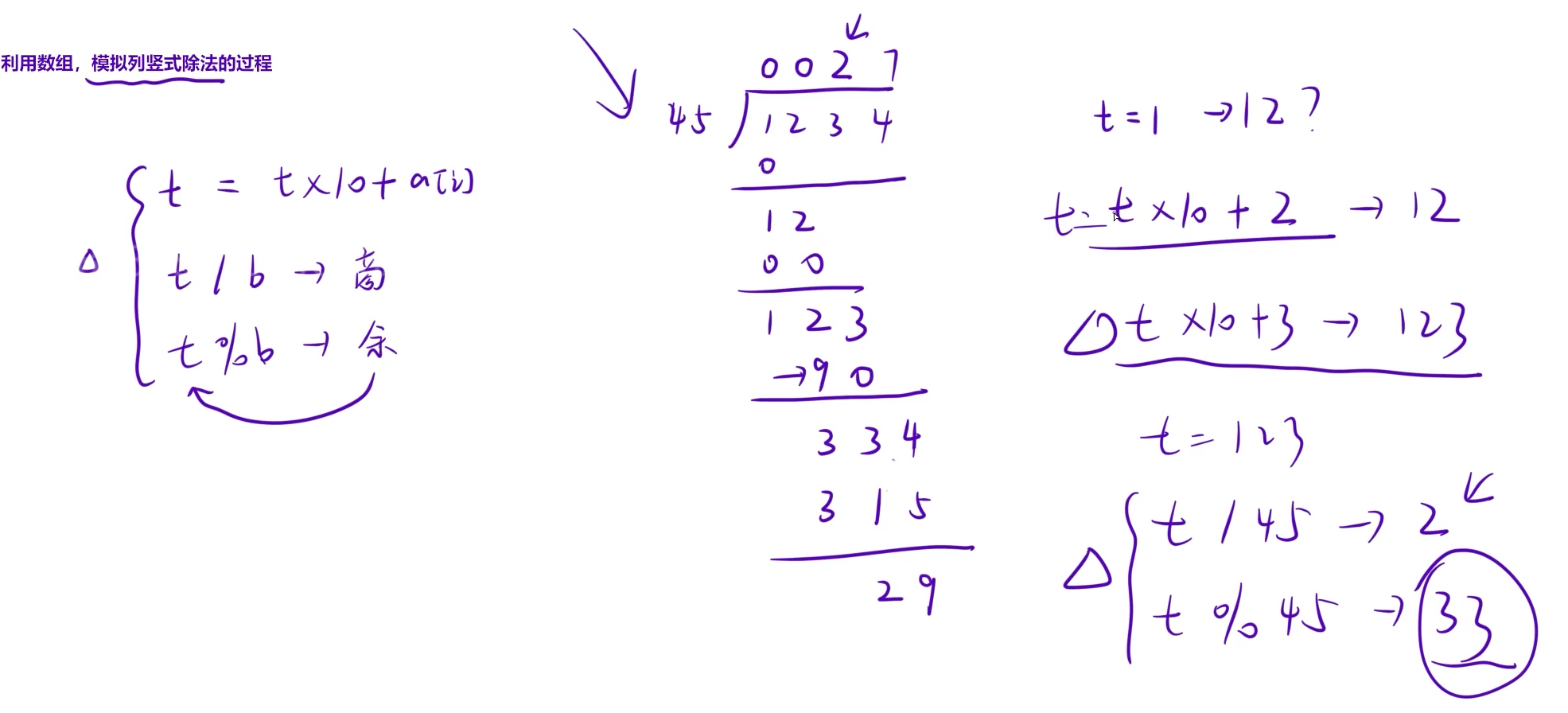
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b, c[N];
int la, lc;
//高精度除法的模板 --- c = a / b (高精度/低精度)
void div(int c[], int a[], int b)
{
long long t = 0; //标记每次除完之后的余数
for (int i = la - 1;i >= 0;i--)
{
//计算当前的被除数
t = t * 10 + a[i];
c[i] = t / b;
t %= b;
}
//处理前导零
while (lc > 1 && c[lc - 1] == 0)
{
lc--;
}
}
int main()
{
string x;
cin >> x >> b;
la = x.size();
lc = la;
for (int i = 0;i < la;i++)
{
a[la - 1 - i] = x[i] - '0';
}
//模拟除法的过程
div(c, a, b); //c = a / b
for (int i = lc - 1;i >= 0;i--)
{
cout << c[i];
}
return 0;
}