数据结构二叉树和BST2

2025-09-19 约 5058 字预计阅读 11 分钟

https://bing.ee123.net/img/rand?artid=151872221

数据结构——二叉树和BST(2)

前言

在计算机科学中，二叉树（Binary Tree）是一种非常重要且基础的数据结构，它为解决层次性、关联性数据问题提供了强大的模型。而二叉搜索树（Binary Search Tree, BST），作为二叉树的一种特例，因其卓越的查找、插入和删除性能，在理论和实践中都占据了核心地位。
本文将深入浅出地解析二叉树和二叉搜索树的核心概念、工作原理及常见操作。无论您是正在学习数据结构的新手，还是希望巩固基础知识的开发者，相信都能从中获益。我们将从最简单的二叉树遍历开始，逐步深入到BST的高效操作，并探讨其性能表现。

一、BST的基本概念

说明：
        二叉搜索树是二叉树的一种重要应用，其主要目的是提供一种高效的数据查找、插入和删除方法。它通过将数据节点按照特定的“排序”规律组织成一棵二叉树，从而利用树形结构的分支特性来大幅减少搜索过程中需要比较的次数，提高搜索效率。
核心性质（“小-中-大”）：
        BST 的核心在于其节点间的排序关系。对于树中的任意一个节点，都必须满足以下条件：
该节点左子树上的所有节点的值都小于或等于该节点本身的值。
该节点右子树上的所有节点的值都大于或等于该节点本身的值。
        这个性质确保了整棵树的数据是有序的。
注意：有些定义要求左子树严格小于，右子树严格大于，即不允许重复值。但在实际应用中，允许“等于”的情况（将等于的节点放在左或右子树均可，需保持一致）也很常见。具体实现时需根据需求确定。
例：
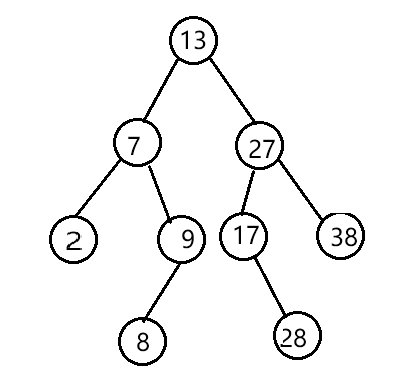
假设我们有一棵已经构建好的 BST，如下图所示（以允许重复值且将等于的节点放在右子树为例）：
查找示例：查找节点 38
从根节点 13 开始比较：38 > 13 -> 根据BST性质，38 只可能出现在根节点 13 的右子树中。我们可以完全忽略整个左子树。
来到右子树的根 27，比较：38 > 27 -> 38 只可能在 27 的右子树中。忽略 27 的左子树。
来到节点 38，比较：38 == 38 -> 查找成功。
优势：在每一步比较后，我们都可以舍弃整个左子树或整个右子树，将搜索范围快速缩小。这种“二分查找”式的策略是其高效的原因。
正因为其强大的查找能力和内在的排序性质，BST也被称为：
二叉排序树 (Binary Sort Tree)
二叉查找树
算法复杂度(时间复杂度)：最糟糕的情形是其退化为链表，最乐观的情形是完美或完全二叉树
最差：T(n) = O(n);
最好：T(n) = O(log2n);

二、BST的基本操作

1、节点设计
2、初始化树节点
3、增删查改
    前提：判断二叉搜索树是否为空
    a、增：插入数据
    b、删：删除数据、销毁二叉搜索树
    c、查：遍历二叉搜索树、获取数据
    d、改：修改数据(基于获取数据基础上))

1、节点设计

说明：

一个数据，两个指针——左子树指针和右子树指针

图解：

代码：

// 二叉搜索树的节点设计
typedef struct node
{
    // 数据域
    datatype data;

    // 指针域
    struct node *lchild_p;  // 左子树指针
    struct node *rchild_p;  // 右子树指针

}node_t, *node_p;

2、初始化树节点

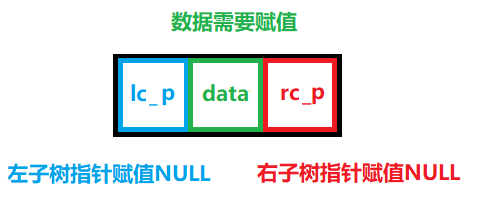
说明:

每一个树节点都是有数据的

图解：

代码：

/**
 * @brief： 初始化树节点
 * @note：  None
 * @param： data：要赋值的数据
 * @retval: 成功：返回指向这个树节点的指针
 *          失败：返回NULL
*/
node_p BST_InitDataNode(datatype data)
{
    // 1、申请树节点堆内存空间
    node_p p = malloc(sizeof(node_t));
    bzero(p, sizeof(node_t));

    // 2、对堆空间进行赋值操作
    if ( p != NULL)
    {
        // 数据域
        p->data = data;

        // 指针域
        p->lchild_p = NULL; // 左子树指针
        p->rchild_p = NULL; // 右子树指针
    }
    else
    {
        return NULL;
    }

    // 3、成功返回指向这个树节点的指针
    return p;
}

3、插入数据

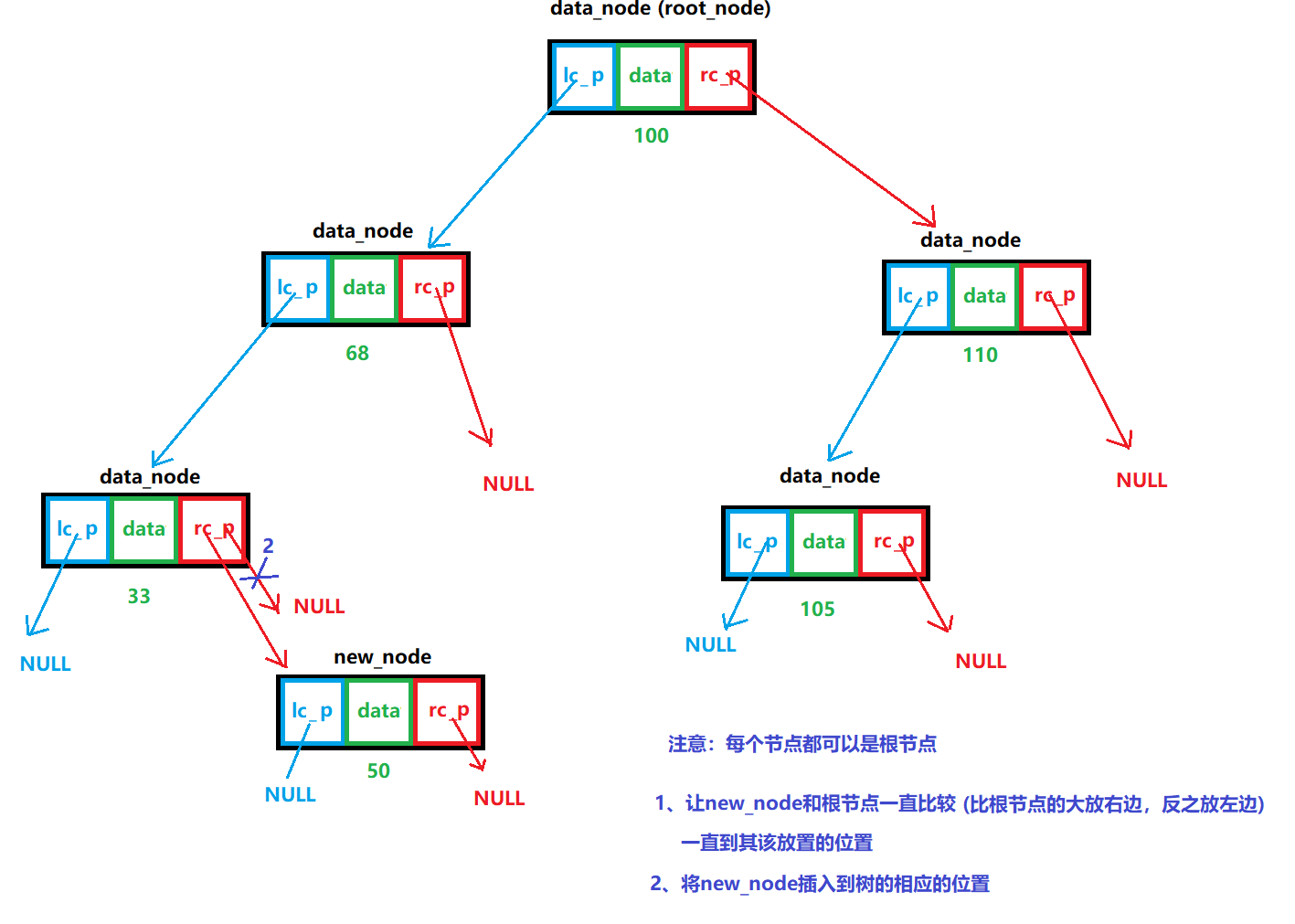
说明：

二叉搜索树，插入数据时，是以递归的方式进行插入的(比根节点数据大小放右边、小的放左边)

图解：

代码：

/**
 * @brief： 插入数据
 * @note：  以二叉排序的方式插入(比根节点数据大的放右边，小的放左边)
 * @param： root_node：根节点
 *          new_node： 要插入的新节点
 * @retval: 成功：返回指向这个树节点的指针
 *          失败：返回NULL
*/
node_p BST_InsertDataNode(node_p root_node, node_p new_node)
{
    // 1、设置退出条件
    if (root_node == NULL)
        return new_node; 

    // 2、比较数据的大小，看数据要插入左子树，还是右子树
    // a、插入左子树
    if ( new_node->data.data < root_node->data.data )
    {
        root_node->lchild_p =  BST_InsertDataNode(root_node->lchild_p, new_node);
    }
    // b、插入右子树
    else if ( new_node->data.data > root_node->data.data )
    {
        root_node->rchild_p =  BST_InsertDataNode(root_node->rchild_p, new_node);
    }
    else
    {
        printf("%d的数据已经存在了，请重新输入!\n", new_node->data.data);
        free(new_node);
    }

    // 3、返回根节点
    return root_node;
}

4、遍历数据

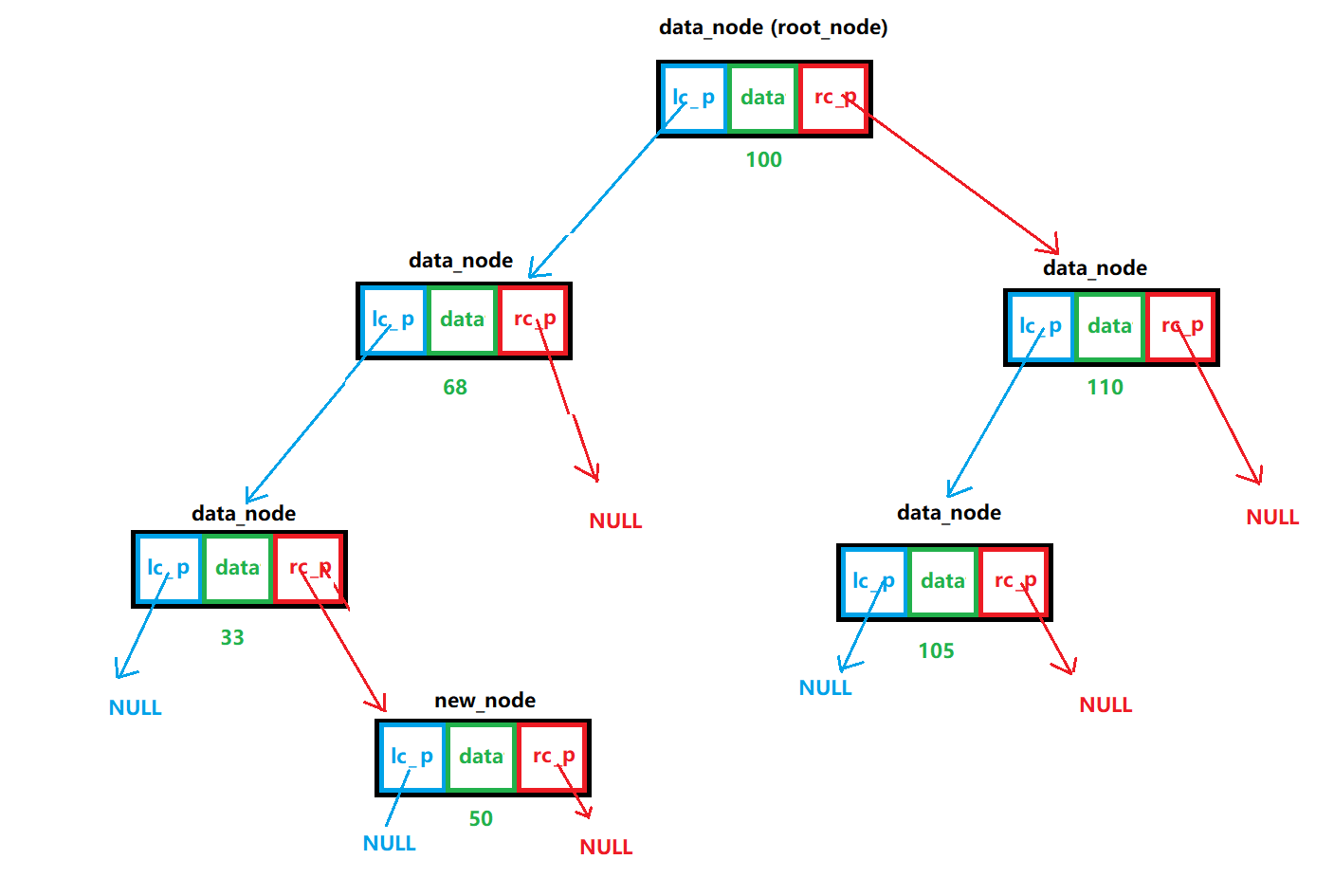
说明：

遍历分为前序遍历(中、左、右)、中序遍历(左、中、右)、后序遍历(左、右、中)、按层遍历

图解：

代码;

/**
 * @brief： 前序遍历
 * @note：  None
 * @param： root_node：根节点
 * @retval: None
*/
void BST_PreorderTraversal(node_p root_node)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)
    if (root_node == NULL)
        return;

    // 2、先访问根节点
    printf("%d\t", root_node->data.data);          // 中

    // 3、再访问左子树、右子树
    BST_PreorderTraversal(root_node->lchild_p);    // 左
    BST_PreorderTraversal(root_node->rchild_p);    // 右
}

/**
 * @brief： 中序遍历
 * @note：  None
 * @param： root_node：根节点
 * @retval: None
*/
void BST_InorderTraversal(node_p root_node)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)
    if (root_node == NULL)
        return;

    // 2、先访问左子树、右子树
    BST_InorderTraversal(root_node->lchild_p);    // 左

    // 3、再访问根节点
    printf("%d\t", root_node->data.data);         // 中

    // 3、再先访问右子树
    BST_InorderTraversal(root_node->rchild_p);    // 右

}

/**
 * @brief： 后序遍历
 * @note：  None
 * @param： root_node：根节点
 * @retval: None
*/
void BST_PostorderTraversal(node_p root_node)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)
    if (root_node == NULL)
        return;

    // 2、再访问左子树、右子树
    BST_PostorderTraversal(root_node->lchild_p);    // 左
    BST_PostorderTraversal(root_node->rchild_p);    // 右

    // 3、先访问根节点
    printf("%d\t", root_node->data.data);           // 中

}

/**
 * @brief： 按层遍历
 * @note：  None
 * @param： root_node：根节点
 * @retval: None
*/
void BST_LevelorderTraversal (node_p root_node)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)
    if (root_node == NULL)
        return;

    // 2、将根节点的数据入队
    _linkqueue p = init_queue();    // 初始化队列结构体
    en_queue(p, root_node);         // 将根节点的数据入队

    // 3、如果链式队列不是空的话，就一直执行下去
    node_p tmp_p = NULL;
    while (!is_empty_q(p))
    {
        // a、出队并访问队头
        out_queue(p, &tmp_p);
        printf("%d\t", tmp_p->data.data);

        // b、依次将左右子树入队
        if (tmp_p->lchild_p != NULL)
        {
            en_queue(p, tmp_p->lchild_p);
        }
        if (tmp_p->rchild_p != NULL)
        {
            en_queue(p, tmp_p->rchild_p);
        } 
    }
}

5、删除数据（*****）

说明：

删除一个BST的节点要比插入困难一点，但同样是要遵循一个原则，即：删除节点后仍然要保持“小-中-大”的逻辑关系。
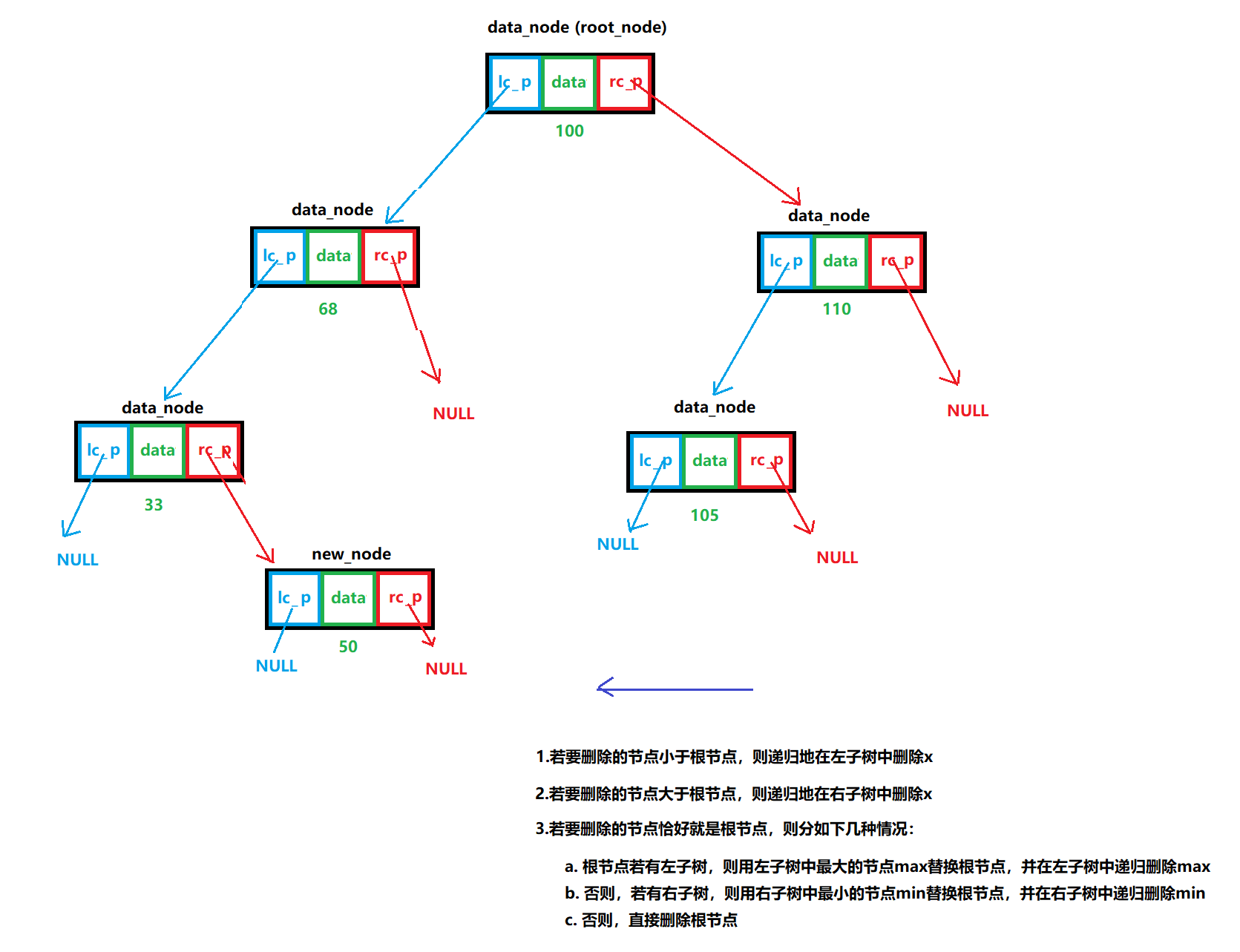
假设要删除的节点是x，大体思路如下：
- 若要删除的节点小于根节点，则递归地在左子树中删除x
- 若要删除的节点大于根节点，则递归地在右子树中删除x
- 若要删除的节点恰好就是根节点，则分如下几种情况：
  - 根节点若有左子树，则用左子树中最大的节点max替换根节点，并在左子树中递归删除max
  - 否则，若有右子树，则用右子树中最小的节点min替换根节点，并在右子树中递归删除min
  - 否则，直接删除根节点
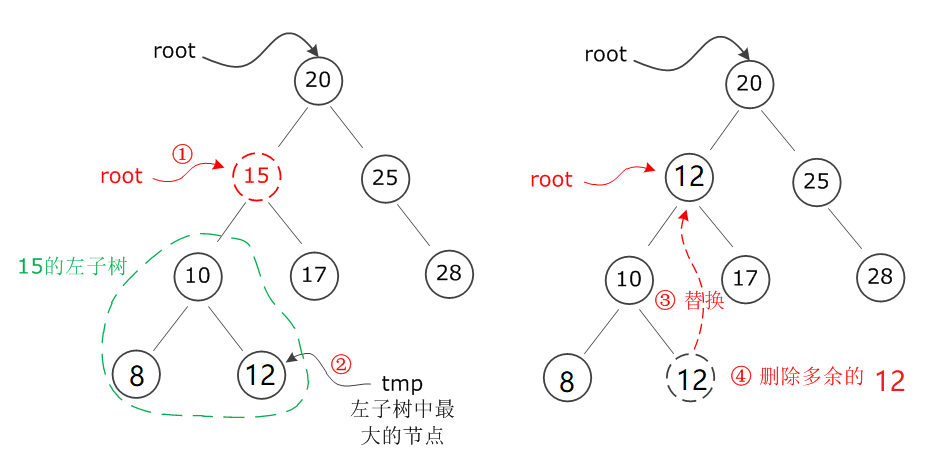
图解1：
以下图为例，假设在一棵二叉树中要删除节点15，在找到节点之后，判断其有左子树，那么就沿着其左子树找到最右下角（最大）的节点12，替换要删除的节点15，然后再将多余的节点12删掉：
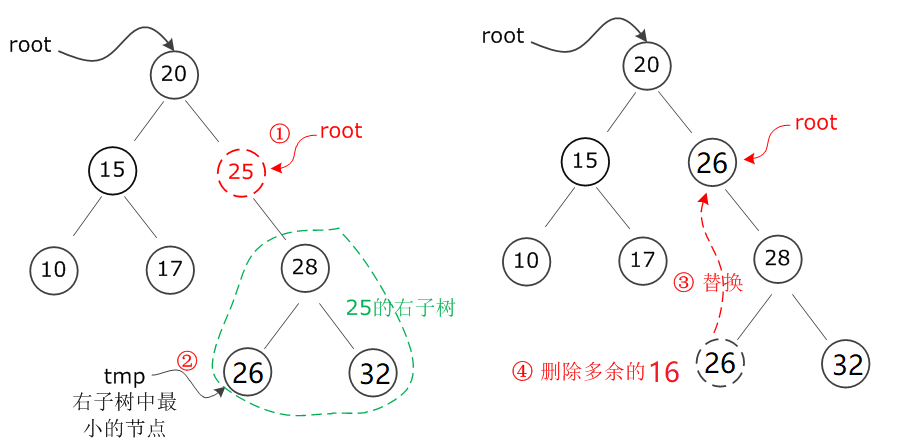
而如果要删除的节点没有左子树，只有右子树，那么情况是完全对称的，如下图所示，假设要删除节点25，由于25没有左子树，因此找到其右子树中最左下角（最小）的节点26，替换要删除的节点25，然后再将多余的节点26删掉：
图解2：
代码：

/**
 * @brief  删除数据
 * @note   None
 * @param  root_node： 根节点
 *         del_data:   要删除的数据
 * @retval 成功：返回指向这个二叉树根节点的指针
 *         失败：返回NULL
 */ 
node_p BST_DelData(node_p root_node, datatype del_data)  // 50
{
    // 1、如果根节点为空，直接返回NULL即可
    if (root_node == NULL)
        return NULL;

    // 2、若data小于根节点，则递归地在左子树上删除它
    if ( del_data.data < root_node->data.data)
    {
        root_node->lchild_p = BST_DelData(root_node->lchild_p, del_data);
    }
    // 3.若要删除的节点大于根节点，则递归地在右子树中删除x

    else if (del_data.data >root_node->data.data)
    {
        root_node->rchild_p = BST_DelData(root_node->rchild_p, del_data);
    }
    // 4.若要删除的节点恰好就是根节点，则分如下几种情况：
    else
    {
        // a、根节点若有左子树，则用左子树中最大的节点max替换根节点，并在左子树中递归删除max
        if (root_node->lchild_p != NULL)
        {
            // 建立中间值(树节点)(左子树最大的节点的值)
            node_p max_node = NULL;

            // 找到左子树最大值
            for (max_node = root_node->lchild_p; max_node->rchild_p!=NULL; max_node=max_node->rchild_p);

            // 将要删除的根节点，和其左子树中的最大值进行交换
            root_node->data.data = max_node->data.data;

            // 将左子树中的最大值删除
            root_node->lchild_p = BST_DelData(root_node->lchild_p, max_node->data);

        }
        // 否则，若有右子树，则用右子树中最小的节点min替换根节点，并在右子树中递归删除min
        else if (root_node->rchild_p != NULL)
        {
            // 建立中间值(树节点)(左子树最大的节点的值)
            node_p min_node = NULL;

            // 找到右子树最大值
            for (min_node = root_node->rchild_p; min_node->lchild_p!=NULL; min_node=min_node->lchild_p);

            // 将要删除的根节点，和其右子树中的最小值进行交换
            root_node->data.data = min_node->data.data;

            // 将右子树中的最小值删除
            root_node->rchild_p = BST_DelData(root_node->rchild_p, min_node->data);
        }
        else
        {   
            free(root_node);
            return NULL;
        }
    }

    // 3、返回root_node
    return root_node;
}

6、获取数据/修改数据

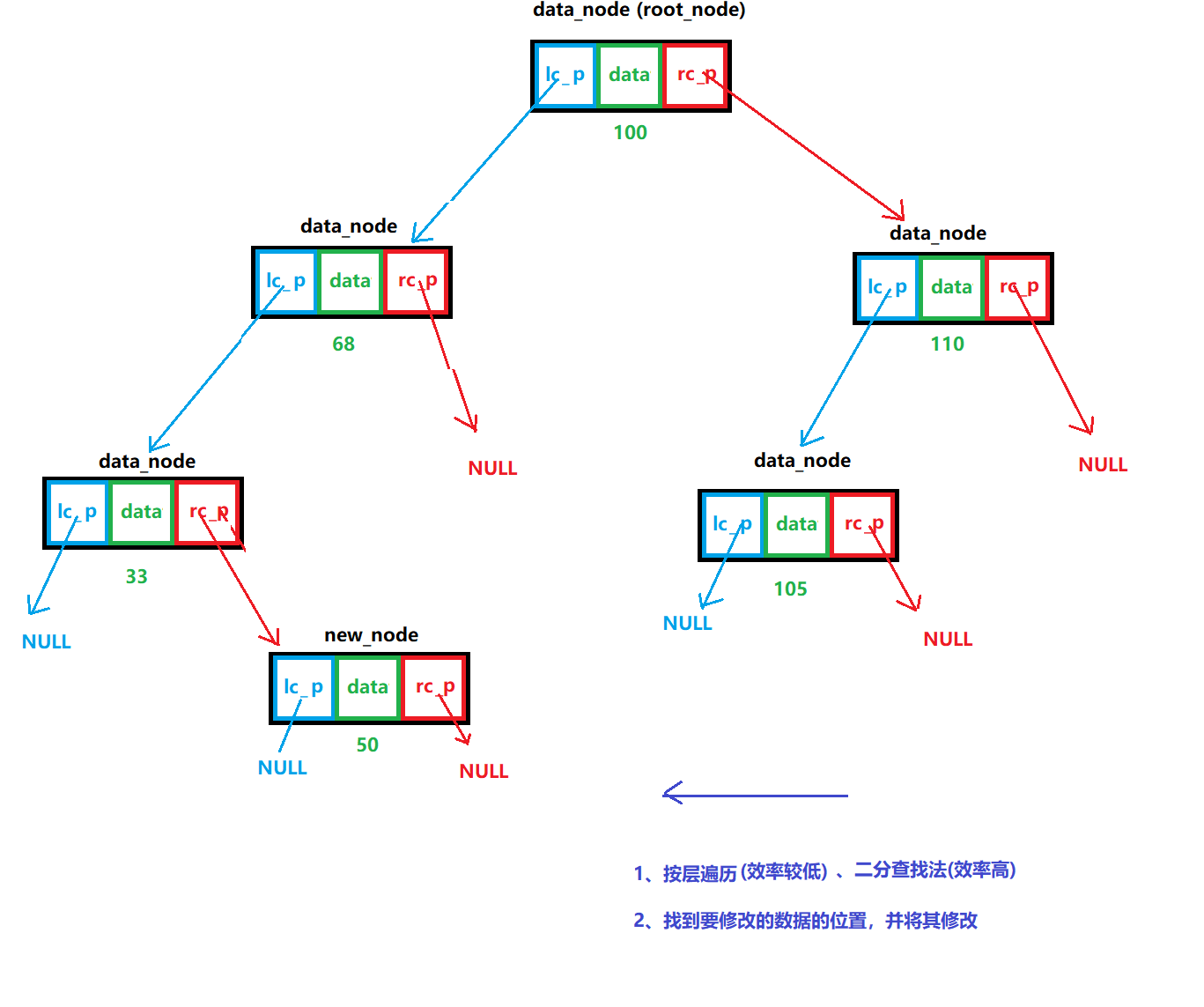
说明：
- 通过遍历或者二分查找法找到获取要找寻的数据(进而也可以修改数据)

图解：

方式一(不推荐，太慢)：使用按层遍历地方式，逐个进行查找数据，并返回数据
方式二(推荐，速度块)：使用二分查找法，进行查找，依据就是，要查找地数据比节点小查其左边，反之右边，依次类推并递归进行即可

代码：

/**
 * @brief： 获取数据(按层遍历二叉树)
 * @note：  通过某个数据(学生id)，找到其它数据(学生其它信息)
 * @param： root_node：根节点
 *          data: 要查找的数据(学生id)
 * @retval: 成功：返回要查找到的数据(包含学生所有信息)
 *          失败：返回NULL
*/

datatype_p BST_TraversalFindData(node_p root_node, datatype data)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)
    if (root_node == NULL)
        return NULL;
    
    // 2、将根节点的数据入队
    _linkqueue p = init_queue();    // 初始化队列结构体
    en_queue(p, root_node);         // 将根节点的数据入队

    // 3、如果链式队列不是空的话，就一直执行下去
    node_p tmp_p = NULL;
    while (!is_empty_q(p))
    {
        // a、出队并访问队头
        out_queue(p, &tmp_p);
        if (tmp_p->data.data == data.data)
        {
            return &(tmp_p->data);
        }

        // b、依次将左右子树入队
        if (tmp_p->lchild_p != NULL)
        {
            en_queue(p, tmp_p->lchild_p);
        }
        if (tmp_p->rchild_p != NULL)
        {
            en_queue(p, tmp_p->rchild_p);
        } 
    }
}


/**
 * @brief： 获取数据(二分查找法)
 * @note：  通过某个数据(学生id)，找到其它数据(学生其它信息)
 * @param： root_node：根节点
 *          data: 要查找的数据(学生id)
 * @retval: 成功：返回要查找到的数据节点(包含学生所有信息)
 *          失败：返回NULL
*/
node_p BST_FindData(node_p root_node, datatype data)
{
    // 1、如果根节点为空，那么就证明执行完了这个二叉树(退出条件)、或者第一个节点就是要找的数据，那就返回root_node本身
    if ( (root_node == NULL) || (root_node->data.data == data.data) )
        return root_node;
    
    // 2、比较大小，递归地进行查找
    if ( data.data < (root_node->data.data) )
    {
        root_node = BST_FindData(root_node->lchild_p, data);
    }
    else
    {
        root_node = BST_FindData(root_node->rchild_p, data);
    }

}

7、销毁BST

说明：

先递归的删除右子树或左子树，最后再删除根节点

图解：

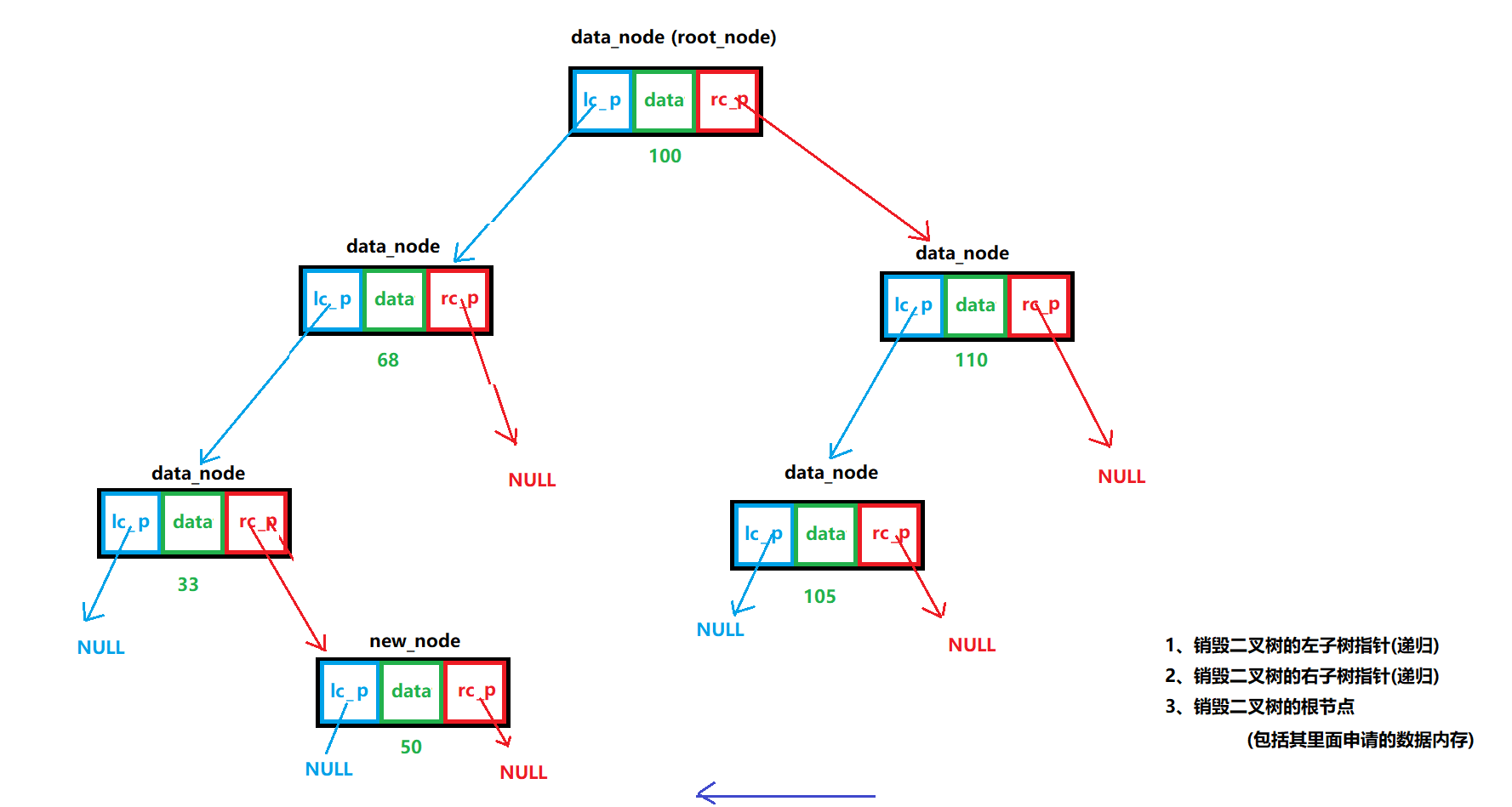
代码：


/**
 * @brief  销毁二叉树
 * @note   None
 * @param  root_node： 根节点
 * @retval None
 */ 
void BST_UnInit(node_p root_node) 
{
    // 1、如果根节点为空，则直接返回即可
    if (root_node == NULL)
        return;

    // 2、递归的销毁左子树
    BST_UnInit(root_node->lchild_p); 

    // 3、递归的销毁右子树
    BST_UnInit(root_node->rchild_p); 

    // 4、销毁根节点
    free(root_node);

}

三、BST的使用

/**
  ******************************************************************************
  * @file    link_cir_queue.h
  * @author  feng
  * @version V0.0.1
  * @date    2025.08.14
  * @brief   二叉搜索树的增删查改功能
  *          环境：ubuntu18.04
  *          编译+执行：./project.sh
  * 
  ******************************************************************************
  * @attention
  *
  *  本文档只供学习使用，不得商用，违者必究
  * 
  *  github：       https://github.com/(求我拿链接)
  *  CSDN:          https://blog.csdn.net/(嘻嘻)
  *  gitee:         https://gitee.com/(求我拿链接)
  *  微信公众号：    没有
  *  没有疑问或者建议：12345678910@qq.com
  * 
  * ******************************************************************************
  */
#include "binary_search_tree.h"
#include "draw_tree.h"

int main(int argc, char const *argv[])
{
    
    // (1)、初始化二叉搜索树的根节点
    datatype data = {0};
    data.data = 100;
    node_p p = BST_InitDataNode(data);
    if (p == NULL)
    {
        printf("初始化二叉树的根节点失败!\n");
        return -1;
    }
    
    // (2)、选择功能(增删查改、退出(销毁二叉搜索树))
    node_p new_node        = NULL;
    int select             = 0;
    datatype   new_data    = {0};
    datatype   del_data    = {0};
    datatype   find_data   = {0};
    node_p     get_data    = NULL;

    // 将之前的html网页删除(如果报没有这个网页可删除问题，无需理会)
    system("rm ./*.html");  
    printf("\n");
    while (1)
    {
        // 1、显示整个二叉搜索树的数据
        printf("===============二叉搜索树中的数据================\n");
        printf("\n前序遍历: \n");
        BST_PreorderTraversal(p);
        printf("\n中序遍历: \n");
        BST_InorderTraversal(p);
        printf("\n后序遍历: \n");
        BST_PostorderTraversal(p);
        printf("\n按层遍历: \n");
        BST_LevelorderTraversal(p);
        printf("\n==============================================\n");

        // 2、显示功能选项
        printf("\n请输入以下功能：\n");
        printf("1、增加数据\n");
        printf("2、删除数据\n");
        printf("3、获取数据(也可以修改数据)\n");
        printf("4、退出!\n");

        // 3、选择要做的功能
        scanf("%d", &select);
        while(getchar()!='\n');

        switch (select)
        {
            case 1:
                // 提示
                printf("请输入要增加的数据：\n");

                // 输入数据
                scanf("%d", &new_data.data);
                while(getchar()!='\n');

                // 生成一个数据节点
                new_node = BST_InitDataNode(new_data);

                // 将新生成的数据节点添加到二叉搜索树中
                BST_InsertDataNode(p, new_node);

                // 画一下网页
                draw_tree(p);

                break;
            case 2:
                // 提示
                printf("请输入要删除的数据\n");

                // 输入数据
                scanf("%d", &del_data.data);
                while(getchar()!='\n');

                // 删除数据
                BST_DelData(p, del_data);

                 // 画一下网页
                draw_tree(p);

                break;

            case 3:
                // 提示
                printf("请输入要获取的数据(相当于你输入了学生的id，获取它的所有信息)\n");

                // 输入数据
                scanf("%d", &find_data.data);
                while(getchar()!='\n');

                // 获取数据
                get_data = BST_FindData(p, find_data);
                printf("get_data.data.data == %d\n", get_data->data.data);

                // 也可以通过这个返回的指针，来修改里面的数据
                // 比如：get_data->data.data = 100;
                break;

            case 4:
                BST_UnInit(p);
                printf("系统已退出！\n");
                goto exit_sys_label;
                break;
           
        }
    }
exit_sys_label: 
    
    return 0;
}

目录