LeetCode算法日记-Day-45-为高尔夫比赛砍树矩阵

目录

LeetCode算法日记 - Day 45: 为高尔夫比赛砍树、矩阵
1. 为高尔夫比赛砍树
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示, 在这个矩阵中:
0表示障碍,无法触碰1表示地面,可以行走比 1 大的数表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 1(即变为地面)。
你将从 (0, 0) 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 -1 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。
示例 1:
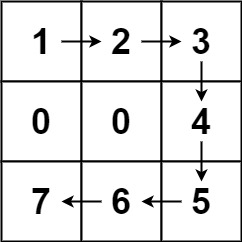
输入:forest = [[1,2,3],[0,0,4],[7,6,5]]
输出:6
解释:沿着上面的路径,你可以用 6 步,按从最矮到最高的顺序砍掉这些树。示例 2:
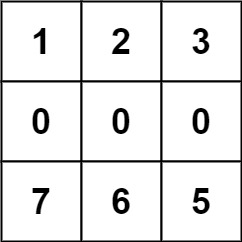
输入:forest = [[1,2,3],[0,0,0],[7,6,5]]
输出:-1
解释:由于中间一行被障碍阻塞,无法访问最下面一行中的树。示例 3:
输入:forest = [[2,3,4],[0,0,5],[8,7,6]]
输出:6
解释:可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树,可以直接砍去,不用算步数。提示:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109
1.1 题目解析
题目本质
- 把可行走网格看作无权图,从起点(0,0)出发,按树高从低到高依次到达每一棵树。
- 每段“从当前点到下一棵树”的最短步数用一次 BFS 求两点最短路,最后把这些最短路长度相加。
- 任意一段不可达则返回 -1。
常规解法
- 直觉:把所有格子值拍平排序,然后对每个目标值在整张图做 BFS 去找同值格子。
问题分析
- 直觉做法会在每个目标值上对大量起点反复 BFS,复杂度接近 O(K × m × n × BFS);
- 同时若用“值相等”判断目标坐标,容易写错索引或被重复值干扰(虽本题树高唯一,但坐标判断更稳)。
- 因此需要把问题拆成“多个两点最短路”。
思路转折
正确路线:
- 先收集所有树的三元组(height,i,j),按 height 升序排序。
- 维护当前坐标(curI,curJ),依次对下一棵树目标坐标(ti,tj)做一次 BFS 求两点最短路;若某次 BFS 返回 -1,则整体 -1;否则累加步数并把当前坐标更新到(ti,tj)。
- 这样每棵树只做一次 BFS,复杂度降为 O(K × m × n),可通过。
1.2 解法
算法思想
- 将“按高度顺序砍树”的全局过程拆为 K 段“从当前点到下一棵树坐标”的两点最短路,每段用 BFS 分层搜索得到最短步数。坐标判断命中目标更安全:到达(ti,tj)即返回当前层数。
i)收集与排序
- 遍历 forest,找出所有 h>1 的格子,记录为 {h,i,j}。
- 对这些三元组按 h 升序排序。
ii)逐树前进
- 设当前坐标(si,sj) 初始为(0,0)。
- 依次取下一棵树目标(ti,tj),调用 BFS 计算从(si,sj) 到(ti,tj) 的最短路。
- 若 BFS 返回 -1,则直接返回 -1;否则将步数累加到答案,并更新(si,sj) = (ti,tj)。
iii)BFS 细节
- 典型四方向分层搜索。
- 起点等于终点时直接返回 0。
- 合法入队条件可合写:边界内、未访问、非障碍。
- 命中条件用坐标判断:nx==ti 且 ny==tj 立即返回当前层步数+1。
易错点
- 目标命中勿写成 forest.get(0).get(b)==cur,应使用坐标命中(nx==ti && ny==tj)。
- visited 不能复用,每次 BFS 都要新建 vis。
- 起点就是目标时要返回 0,避免多走一层。
- 如果使用合并判断条件写法,注意顺序与短路:边界检查应放在最前,否则会数组越界。
1.3 代码实现
import java.util.*;
class Solution {
// 定义方向数组:上下左右四个方向
int[] dx = {0,0,-1,1};
int[] dy = {1,-1,0,0};
int m,n;
public int cutOffTree(List<List<Integer>> forest) {
m = forest.size();
n = forest.get(0).size();
int result = 0;
int si = 0, sj = 0;
// 获取树:收集所有高度>1的单元格
// 新数组列表与原数字建立映射
List<int[]> listNum = new ArrayList<>();
for(int i = 0; i < m ; i++){
for(int j = 0; j < n ; j++){
int h = forest.get(i).get(j);
if(h > 1) listNum.add(new int[]{h,i,j});
}
}
// 树排序:按高度升序
listNum.sort(Comparator.comparingInt(a -> a[0]));
// 进行遍历
// si, sj 表示当前要进行 bfs 的格子坐标
// ti, tj 表示要搜索的目标树坐标
for(int[] t : listNum){
int ti = t[1], tj = t[2];
// 因为要从 forest 拿值, 所以方法需要传入 forest
int tmp = bfs(forest, si, sj, ti, tj);
// 因为0是有效值, 所以判断的时候使用-1来标记违法值
if(tmp == -1) return -1;
result += tmp;
// 赋值到刚查到的最小树, 才能实现最少步骤完成任务
si = ti;
sj = tj;
}
return result;
}
// BFS 求两点最短路
public int bfs(List<List<Integer>> forest, int si, int sj, int ti, int tj){
// 如果起点和终点相同, 不用走
if(si == ti && sj == tj) return 0;
// 用于标记每一次遍历的监察数据, 涉及到多次调用不能污染 vis
boolean[][] vis = new boolean[m][n];
// 用于存储当前 si, sj 所代表的要进行 bfs 遍历的格子
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{si,sj});
vis[si][sj] = true;
int step = 0;
while(!q.isEmpty()){
int size = q.size();
// 按层进行划分
for(int i = 0; i < size; i++){
int[] num = q.poll();
int a = num[0], b = num[1];
// 如果到达目标坐标, 返回当前步数
if(a == ti && b == tj) return step;
for(int j = 0 ; j < 4 ; j++){
int x = a + dx[j], y = b + dy[j];
// 边界内 + 非障碍 + 未访问 才能入队
if(x>=0 && x<m && y>=0 && y<n && forest.get(x).get(y) != 0 && !vis[x][y]){
q.offer(new int[]{x,y});
vis[x][y] = true;
}
}
}
step++;
}
// 无法到达目标
return -1;
}
}复杂度分析
- **时间:**排序 O(K log K);每棵树一次 BFS,最坏 O(mn),合计 O(K × m × n)(K 为树数,K ≤ m×n)。
- **空间:**visited 与队列最坏 O(mn)。
2. 矩阵
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
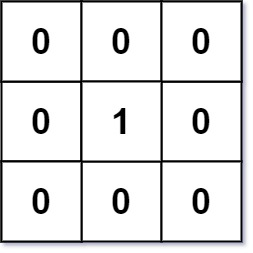
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]示例 2:
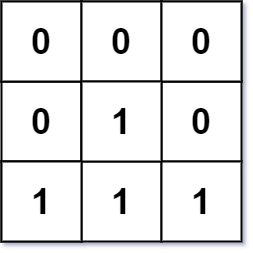
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat中至少有一个0
2.1 题目解析
题目本质
- 在无权网格图上求“到最近 0 的距离”。把所有 0 当作同时出发的源点,向外分层扩散,到达每个 1 的最早层数就是最短距离。换句话说,这是一个多源 BFS问题。
常规解法
- 对每个为 1 的格子各自做一次 BFS 去找最近的 0。每次命中即返回该距离。
问题分析
- 对每个 1 都独立 BFS 会重复遍历大量相同区域,最坏要做 O(mn) 次 BFS,每次 O(mn),总体 O((mn)²),会超时。
- 观察到“距离最近的 0”天然满足“波前最先到达即最短路”的性质,因此应把所有 0 一起作为源点做一次搜索。
思路转折
- 要想高效 → 必须把“从每个 1 找 0”的思路反过来,改成“从所有 0 同时出发填充距离”。
- 具体做法:把所有为 0 的格子先入队并标记已访问,按层向四周扩散。队列每推进一层,邻居的距离就加一。这样每个格子只会被入队一次,总复杂度 O(mn)。
2.2 解法
算法思想
使用多源 BFS:
- 初始时将所有值为 0 的坐标入队并标记已访问;
- 逐层弹出当前层的所有点,把尚未访问的合法邻居入队,其距离 = 当前层层号;
- 直到队列为空。每个点第一次被访问到的层号就是它到最近 0 的最短距离。
i)预处理
- 记录矩阵行列 m、n。
- 创建 vis[m][n] 访问数组。
- 创建队列 q,把所有 mat[i][j]==0 的坐标入队并置 vis[i][j]=true。
- 准备方向数组 dx, dy。
ii)分层 BFS
维护 step 表示当前扩散层的距离,初值为 1(因为 0 自身距离是 0,下一圈邻居距离为 1)。
循环直到队列为空:
- 取出当前层 size 个点,逐个向四邻扩展;
- 对每个邻居(x,y),若在边界内、未访问,则入队并标记已访问,同时将 mat[x][y] 赋为 step;
- 直当前层处理完毕,step++。
iii)返回
- 队列耗尽后,mat 即为目标矩阵,返回它。
易错点
- 不要对每个 1 单独 BFS,会超时。应把所有 0 一次性入队做多源 BFS。
- 访问标记 vis 必须在入队时就置为 true,否则同一节点会被多次入队,导致重复计算。
- 分层计数 step 的更新应在一整层处理完成后自增,这样入队的邻居距离才准确。
- 合法性检查的顺序建议先做边界检查,再判访问与障碍,避免越界访问数组。
- 如果原地写回距离,初始为 0 的位置不要被覆盖;本解法只在首次访问邻居时写距离,不会覆盖 0。
2.3 代码实现
import java.util.*;
class Solution {
int m, n;
boolean[][] vis;
int[] dx = {0, 0, -1, 1};
int[] dy = {1, -1, 0, 0};
public int[][] updateMatrix(int[][] mat) {
m = mat.length;
n = mat[0].length;
vis = new boolean[m][n];
Queue<int[]> q = new LinkedList<>();
// 多源入队:所有 0 作为起点,距离为 0,已访问
for (int i = 0 ; i < m; i++) {
for (int j = 0; j < n; j++) {
if (mat[i][j] == 0) {
q.offer(new int[]{i, j});
vis[i][j] = true;
}
}
}
int step = 1; // 第一层邻居距离为 1
while (!q.isEmpty()) {
int size = q.size();
// 分层遍历
while (size-- != 0) {
int[] cur = q.poll();
int a = cur[0], b = cur[1];
// 扩展四邻
for (int k = 0; k < 4; k++) {
int x = a + dx[k], y = b + dy[k];
// 合法且未访问的邻居才入队,并设置距离
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
q.offer(new int[]{x, y});
vis[x][y] = true;
mat[x][y] = step; // 到最近 0 的距离
}
}
}
step++; // 下一层的距离 +1
}
return mat;
}
}复杂度分析
- 时间复杂度:O(mn)。每个格子最多入队一次,四邻检查的总次数与边数同阶,整体线性于格子数。
- 空间复杂度:O(mn)。队列与 visited 最坏情况下同时占用 O(mn) 空间。
