java后端工程师进修ing研一版day44

目录

java后端工程师进修ing(研一版‖day44)
今日总结
- java随征录——kafka(完结)
- 科研随探录——
- 八股随笔录——MySQL面试篇(6/7)
- 代码随想录——构造平衡二叉搜索树
详细内容
java随征录
kafka自动生成的data目录是用来干什么的
存储数据的核心位置,保存的数据和文件如下
- 日志段文件
Kafka的消息是以日志的形式存储的,每个分区由多个日志段文件组成。.log文件是实际存储消息的文件,.index文件是偏移量索引文件,.timeindex文件是时间戳索引文件
- 事务日志文件
如果Kafka开启了事务功能,那么在 data 目录下会有事务日志文件
- 分区元数据文件
存储分区的相关信息
- 日志清理相关文件
Kafka为了控制磁盘空间的使用,会定期进行日志清理操作。在文件中记录那些日志段被清理过,那些还需要清理
Broker启动的流程
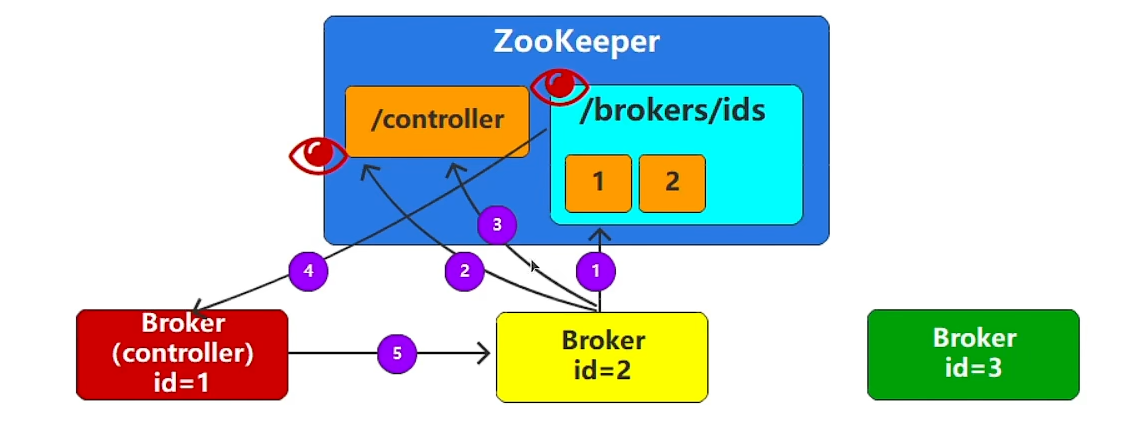
- 注册Breoker节点
- 监听/controller节点
- 注册/controller节点
- 通知集群的变化
- 连接Broker,发送集群的相关数据
科研随探录
八股随笔录
- mysql里的锁
全局锁:会将整个数据库处于只读状态,其他线程一下操作处于堵塞状态。
表级锁:有以下几种
表锁:表锁会限制别的线程的操作,还会限制本线程接下来的读写操作
元数据锁:当对数据库表进行操作时,会自动给这个表加上MDL、
意向锁:
行级锁:InnoDB引擎是支持行级锁的
记录锁:锁住的是一条记录
间隙锁:只存在于可重复读隔离级别,为了解决可重复读隔离级别下幻读的现象
临键锁:锁定一个范围,并锁定记录本身。
- 日志文件
redo log重做文件:是InnoDB存储引擎生成的日志,实现了事务的持久性,只要用于故障恢复
undo log回滚日志:是InnoDB存储引擎层生成的日志,实现了十五中的原子性,
bin log二进制日志:是server层生成的日志,用于数据备份和主从复制
relay log中继日志:用于主从复制场景下
5.慢查询日志
代码随想录
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
示例 1:
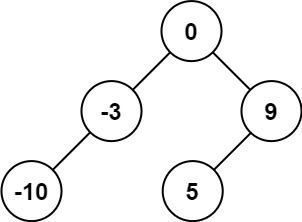
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案: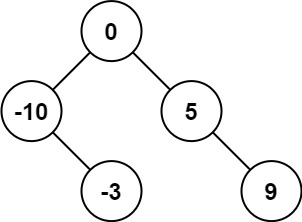
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// int length = nums.length;
// TreeNode root = new TreeNode(nums[length/2]);
// int i = 0;
// public TreeNode sortedArrayToBST(int[] nums) {
// if(i == length/2) {
// i++;
// }
// if(root.val > nums[i]) {
// TreeNode node = new TreeNode(nums[i]);
// i++;
// root.left = node;
// return new TreeNode sortedArrayToBST(nums);
// }
// if(root.val < nums[i]) {
// TreeNode node = new TreeNode(nums[i]);
// i++;
// root.right = node;
// return new TreeNode sortedArrayToBST(nums);
// }
// if(i == nums.length) {
// return root;
// }
// }
public TreeNode sortedArrayToBST(int[] nums) {
return dfs(nums,0,nums.length - 1);
}
public TreeNode dfs(int[] nums, int left, int right) {
if(left > right) {
return null;
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = dfs(nums,left,mid - 1);
root.right = dfs(nums,mid + 1,right);
return root;
}
}