第一章 神经网络的复习

1.1 数学和python的复习

1.1.1 向量和矩阵

向量是同时拥有大小和方向的量
向量可以表示为排成一排的数字集合，在 Python 实现中可以处理为一维数组。

( 1 2 3 ) \begin{pmatrix} 1 \ 2 \ 3 \ \end{pmatrix}

​123​

​

矩阵是排成二维形状（长方阵）的数字集合。

( 1 2 3 4 5 6 ) \begin{pmatrix} 1 & 2 \ 3 & 4 \ 5 & 6 \end{pmatrix}

​135​246​

​
水平方向上排列称为行(row),垂直方向上的排列称为列(column);以下矩阵称为"3行2列的矩阵",记为"3x2的矩阵"

使用python对话模式来生成向量和矩阵: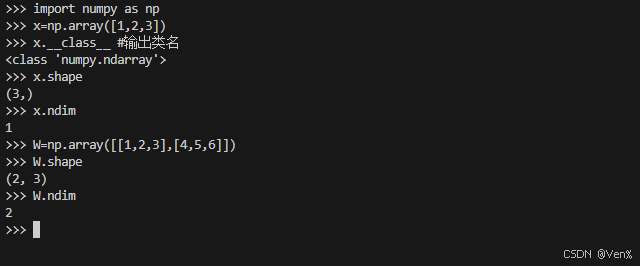

1.1.2 矩阵对应元素的运算

对应多维数组中的元素（独立）进行的，这就是 NumPy 数组中的对应元素的运算。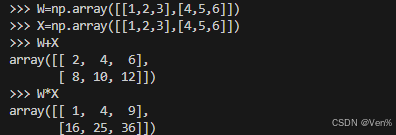

1.1.3 广播

在Numpy多维数组中,形状不同的数组之间也可以进行运算: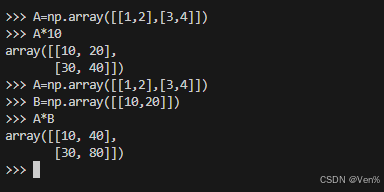

1.1.4 向量内积和矩阵乘积

向量内积:两个向量对应元素的乘积之和

x ⋅ y

( x 1 , ⋯   , x n ) ⋅ ( y 1 , ⋯   , y n )

x 1 y 1 + x 2 y 2 + ⋯ + x n y n \mathbf{x} \cdot \mathbf{y} = (x_1, \cdots, x_n) \cdot (y_1, \cdots, y_n)=x_1 y_1 + x_2 y_2 + \cdots + x_n y_n x⋅y=(x1​,⋯,xn​)⋅(y1​,⋯,yn​)=x1​y1​+x2​y2​+⋯+xn​yn​

(看到第六页)