数据结构双向链表


数据结构——双向链表
目录
前言
在计算机科学的广阔领域中,数据结构是构建高效、可靠软件的核心基石。当我们谈论线性数据结构时,链表凭借其动态内存管理的天然优势,成为了不可或缺的一环。而在链表的家族中,双向链表(Doubly Linked List) 无疑是一位兼具灵活性与实用性的重要成员。
与单向链表不同,双向链表的每个节点都包含了两个指针:一个指向它的后继节点(
next),另一个指向它的前驱节点(prev)。这一看似微小的结构改变,带来了质的飞跃。它使得链表不仅可以单向顺序访问,还能支持反向遍历,这为许多操作带来了极大的便利。例如,在已知某个节点的情况下,删除它不再需要从头遍历以定位其前驱节点,从而将时间复杂度降至常数级 O(1)。这种特性使其成为实现浏览器历史记录、LRU缓存淘汰算法等高级功能的理想选择。然而,“天下没有免费的午餐”。双向链表带来的操作便利性是以更高的空间复杂度(每个节点多一个指针)和更复杂的指针维护逻辑为代价的。正因如此,透彻理解其工作原理并准确无误地实现指针的指向更新,是每一位开发者必须掌握的硬核技能。
为帮助大家系统性地攻克这一知识点,本文将摒弃浮于表面的概念叙述,采取实战驱动的方式,深入浅出地解析双向链表的核心操作。我们将使用清晰的代码示例(语言无关,着重逻辑),逐步演示并详解如何实现对双向链表的:
- 增(Insertion):如何在链表头部、尾部及任意中间位置插入新节点。
- 删(Deletion):如何安全、高效地删除指定节点,并妥善处理边界条件。
- 改(Update):如何查找目标节点并修改其存储的数据。
- 查(Retrieval):如何正向与反向遍历链表,以及按值或按位置进行查找。
无论您是正在备战技术面试的学生,还是希望夯实基础、追求代码卓越的工程师,本文都将为您提供一份逻辑严谨、内容详实的实践指南。让我们一同揭开双向链表的神秘面纱,掌握其精妙之处,从而在复杂的系统设计中能够游刃有余地选择并应用最合适的数据结构。
现在,请随我开始这场探索之旅。
一、双向链表
(1)基本概念
双向链表(Doubly Linked List)是一种更复杂的链表结构。与单向链表不同,它的每个节点包含两个指针域:一个指向其直接后继节点(
next),另一个指向其直接前驱节点(prev)。这一特性使得从任意一个节点出发,都可以方便地访问它的前驱节点和后继节点,从而实现双向遍历。在实际应用中,双向循环链表(Doubly Circular Linked List) 是最常见和便捷的形态。它将头节点的前驱(
prev)指向尾节点,同时将尾节点的后继(next)指向头节点,形成一个闭环。这种设计极大地提升了操作的灵活性,例如反向遍历、在尾部进行插入删除等操作都变得非常高效,时间复杂度可降至 O(1)。图解:
(2)双向链表的设计
这里以实现怎删改查为例:
1、节点设计 2、初始化空双向链表(初始化头节点) 3、初始化数据节点 4、增删查改双向链表 // 前提:判断链表是否为空 a、增:插入数据(头插法、尾插法) b、删:删除数据、销毁链表 c、查:遍历链表 d、改:修改数据
1、节点设计‘
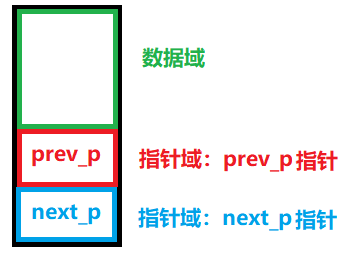
双向链表(Doubly Linked List)的节点结构是其实现双向遍历能力的基石。与单向链表(Singly Linked List)的节点相比,双向链表的节点核心区别在于多了一个指向前驱节点(previous node)的指针
个标准的双向链表节点包含三个成员:
data:存储节点所承载的实际数据元素。其类型可以是任意需要存储的数据类型(如整数、字符串、对象等)。prev:指针(或引用)。指向当前节点的前一个节点(前驱节点)。对于链表头部的节点,在非循环结构中,其prev通常指向null。next:指针(或引用)。指向当前节点的后一个节点(后继节点)。对于链表尾部的节点,在非循环结构中,其next通常指向null。图解:
示例代码:
typedef struct node { int data; struct node *next_p; struct node *prev_p; } node_t, *node_p;
2、初始化空双向链表(初始化头节点)
在双向链表的实现中,引入一个头节点(Head Node)(也称为哨兵节点 - Sentinel Node)是一种常见且高效的设计技巧。这个头节点本身不存储任何实际的有效数据,它的唯一作用是作为链表的一个固定入口点,用于简化边界条件的处理。
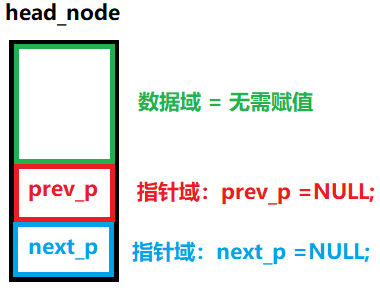
初始化一个空的双向链表,意味着:
- 创建一个头节点。
- 将这个头节点的
prev指针和next指针都设置为NULL(或None等,表示空)。- 此时,链表的结构为:
Head -> NULL。头节点是链表中唯一的节点,它既是开始也是结束。图解:
示例代码:
/** * @brief: 初始化空双向链表(初始化头节点) * @note: None * @param: None * @retval: 成功:返回指向这个头节点的指针 * 失败:返回NULL */ node_p dlink_list_Init(void) { node_p p=malloc(sizeof(node_t)); bzero(p,sizeof(node_t)); if (p!=NULL) { //数据域 无需赋值 //指针域 p->prev_p=NULL; //如果是双向循环链表 p->prev_p=p; p->next_p=p; p->next_p=NULL; } else { return NULL; } return p; }
3、初始化数据节点
数据节点是双向链表中实际存储数据的单元。当我们需要向链表中添加新数据时,首先要创建一个新的数据节点。
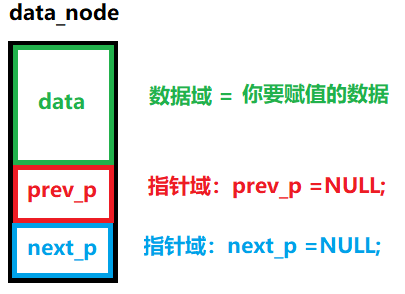
初始化一个数据节点意味着:
- 在内存中分配空间创建一个新节点。
- 将需要存储的数据赋值给节点的
data域。- 将节点的
prev指针和next指针都初始化为NULL(或None等)。- 此时,该节点是一个独立的、未链接到任何链表中的节点。
图解:
示例代码:
/** * @brief: 初始化数据节点 * @note: None * @param: data:要赋值的数据 * @retval: 成功:返回指向这个头节点的指针 * 失败:返回NULL */ node_p dlink_list_InitDataNode(int data) { node_p p=malloc(sizeof(node_t)); bzero(p,sizeof(node_t)); if (p!=NULL) { //数据域 p->data=data; //指针域 //如果是双向循环链表 p->next_p=NULL; // p->prev_p=p; p->prev_p=NULL; // p->next_p=p; } else { return NULL; } return p; }
4、判断链表是否为空
对于使用头节点(哨兵节点)的双向链表,判断链表是否为空的逻辑非常简单且统一。由于头节点始终存在,我们不需要检查头节点本身是否为
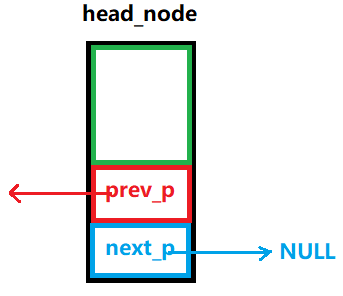
NULL,而是检查头节点是否"链接"了任何实际的数据节点。判断条件:
- 如果**头节点的
next指针指向NULL且头节点的prev指针也指向NULL(**在非循环结构中),说明链表为空。图解:
示例代码:
/** * @brief: 判断链表是否为空 * @note: None * @param: head_node:头节点 * @retval: 成功:返回true * 失败:返回false */ bool dlink_list_IsEmpty(node_p head_node) { return((head_node->next_p==NULL) &&(head_node->prev_p==NULL)); }
5、插入数据(头插法、尾插法)
在带头节点的双向链表中插入新节点,有两种基本方式:
- 头插法:将新节点插入到头节点之后,成为新的第一个数据节点
- 尾插法:将新节点插入到链表尾部,成为新的最后一个数据节点
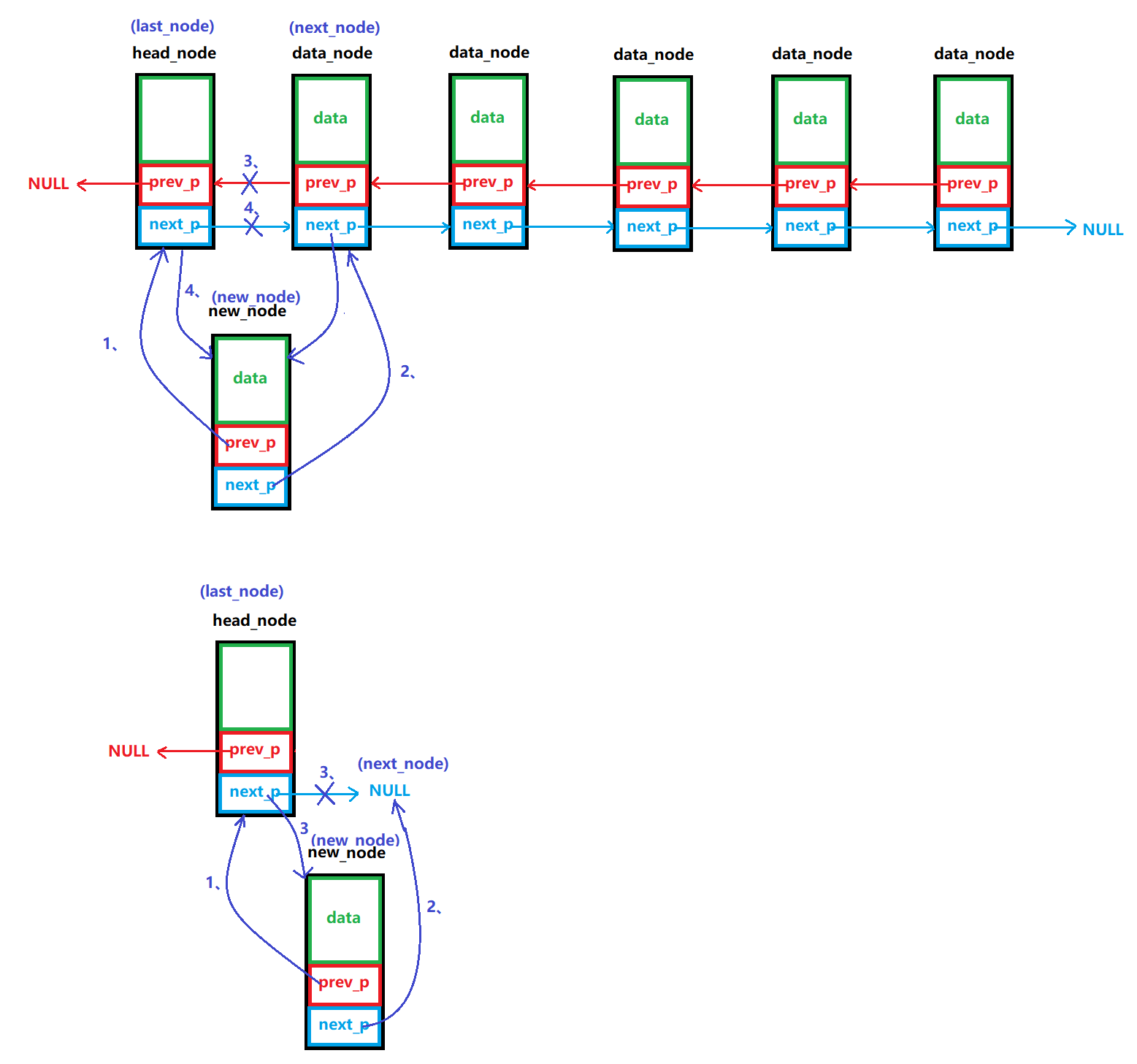
头插法(Head Insertion)
步骤:
- 创建新节点
- 将新节点的
next指向原第一个节点- 将新节点的
prev指向头节点- 如果链表非空,将原第一个节点的
prev指向新节点- 将头节点的
next指向新节点图解:
头插法
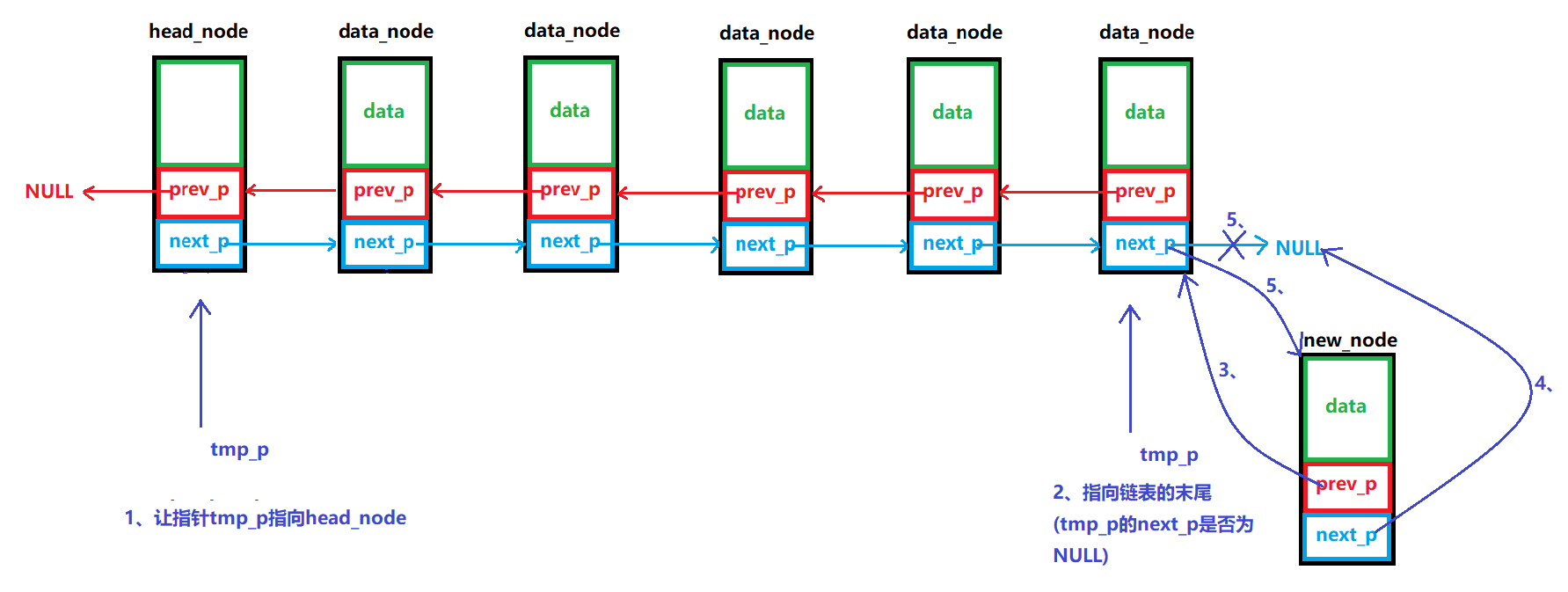
尾插法(Tail Insertion)
步骤:
- 创建新节点
- 找到最后一个节点(尾节点)
- 将尾节点的
next指向新节点- 将新节点的
prev指向尾节点- 将新节点的
next指向 NULL(或尾哨兵节点)图解:
尾插法:
示例代码:
/** * @brief: 插入数据(头插法) * @note: None * @param: head_node:头节点, new_node:要插入的新节点 * @retval: none */ void dlink_list_headInsert(node_p head_node,node_p new_node) { if(dlink_list_IsEmpty(head_node)) { new_node->prev_p=head_node; new_node->next_p=NULL; head_node->next_p=new_node; } else{ new_node->prev_p=head_node; new_node->next_p=head_node->next_p; head_node->next_p->prev_p=new_node; head_node->next_p=new_node; } }/** * @brief: 插入数据(尾插法) * @note: None * @param: head_node:头节点, new_node:要插入的新节点 * @retval: none */ void dlink_list_tailInsert(node_p head_node,node_p new_node) { node_p tmp_p=NULL; for(tmp_p=head_node;tmp_p->next_p!=NULL;tmp_p=tmp_p->next_p); new_node->prev_p=tmp_p; new_node->next_p=NULL; tmp_p->next_p=new_node; }
6、遍历链表
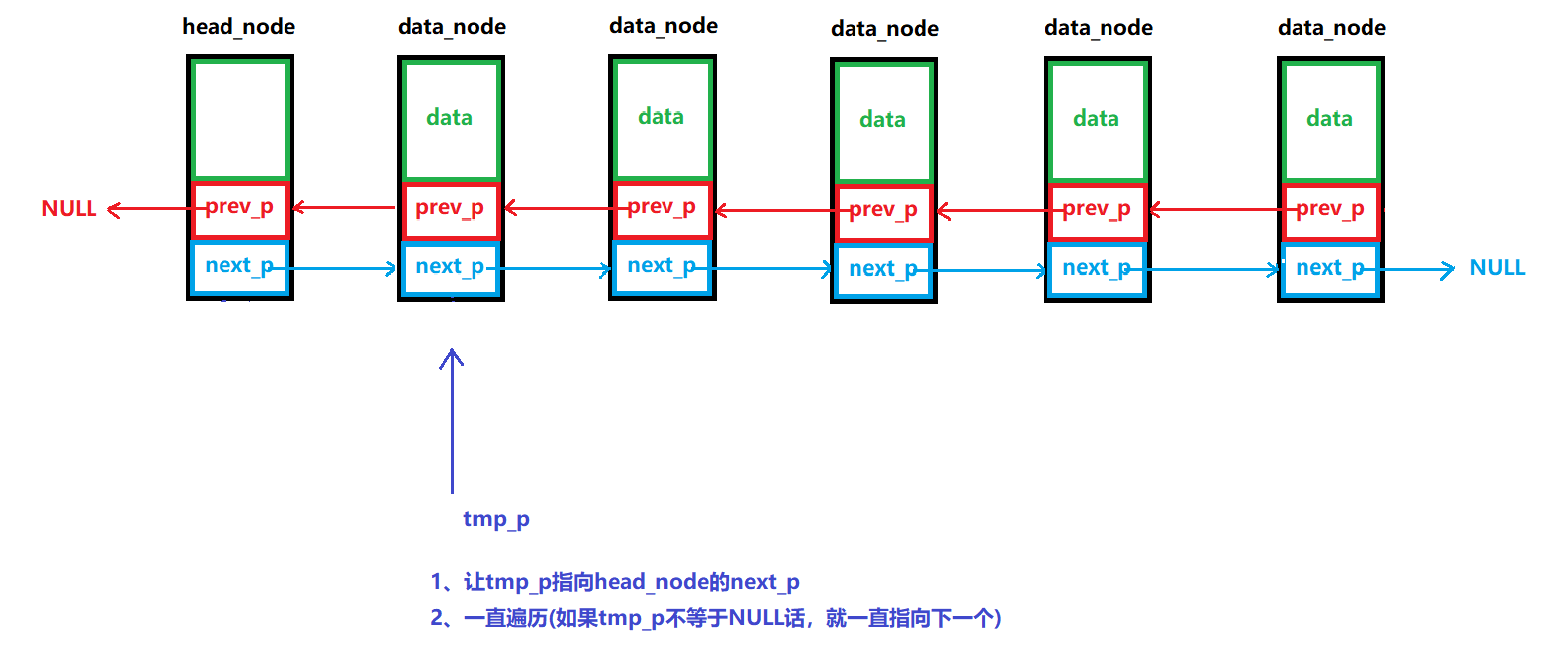
双向链表由于其独特的结构(每个节点都有前驱和后继指针),支持两种遍历方式:
- 正向遍历:从头节点开始,沿着
next指针方向遍历到链表尾部- 反向遍历:从尾节点开始,沿着
prev指针方向遍历到头节点图解:
示例代码:
/** * @brief: 遍历链表的数据 * @note: 从头到尾遍历 * @param: head_node:头节点 * @retval: None */ int dlink_list_ShowList(node_p head_node) { // 1、判断链表是否为空,是的话,返回-1 if (dlink_list_IsEmpty(head_node)) return -1; // 2、遍历整个链表,并打印里面的节点的数据 node_p tmp_p = NULL; int i = 0; printf("======================链表中的数据==========================\n"); for ( tmp_p = head_node->next_p; tmp_p!=NULL; tmp_p=tmp_p->next_p) { printf("链表中的第%d的节点, 数据为: %d\n", i, tmp_p->data); i++; } printf("===========================================================\n"); // 3、成功返回0、 return 0; }
7、删除数据
根据数据值删除链表中的节点是双向链表的常见操作。由于双向链表的节点包含前驱指针,删除操作相比单向链表更加高效,特别是当已经定位到要删除的节点时,可以在 O(1) 时间内完成删除。
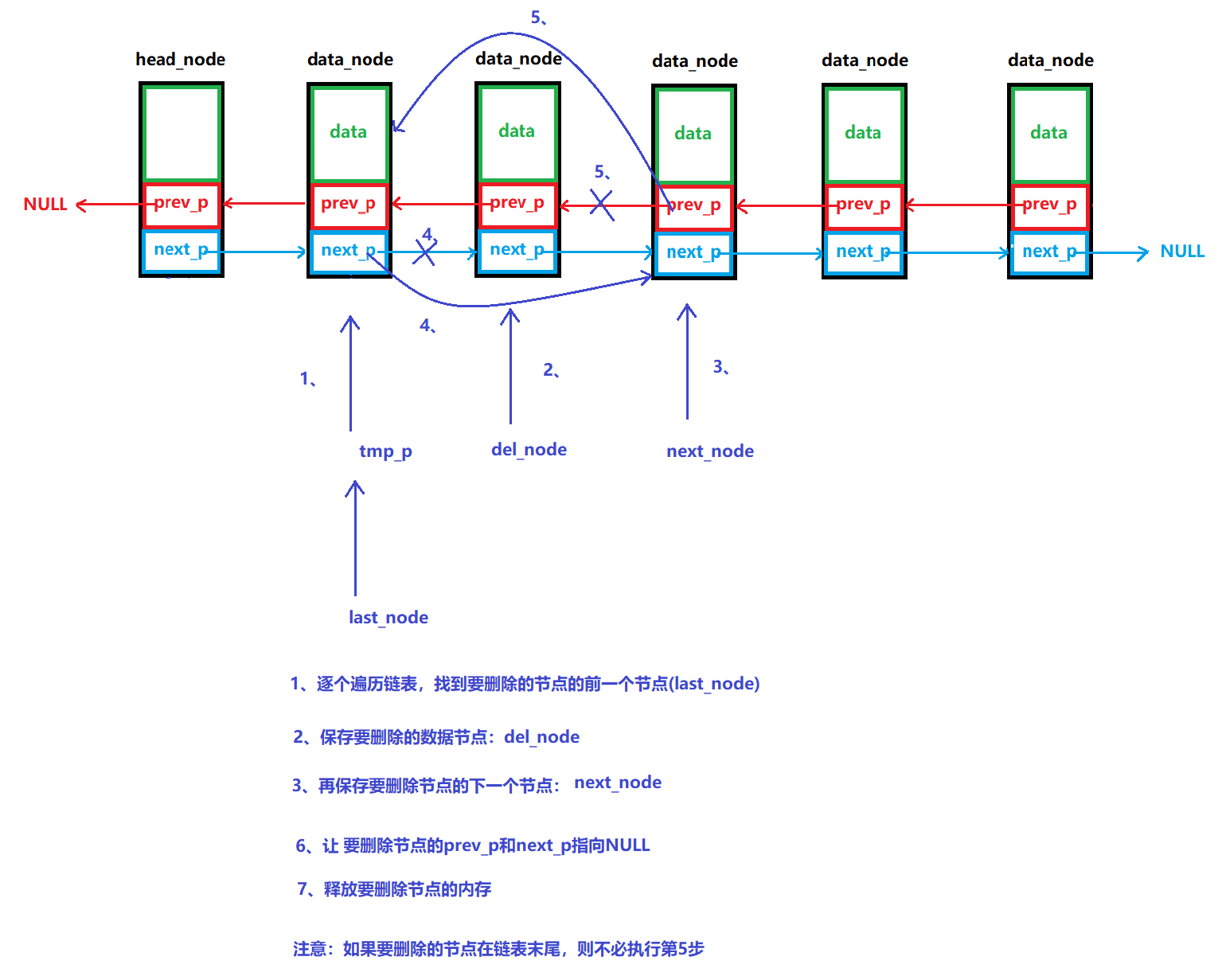
删除步骤:
- 查找节点:遍历链表,找到包含目标数据的节点
- 调整指针:修改该节点前驱和后继节点的指针,绕过要删除的节点
- 释放内存:释放被删除节点的内存空间
- 更新元数据:更新链表大小等元数据
特殊情况处理:
- 空链表:直接返回
- 未找到目标数据:返回错误信息
- 删除头节点后的第一个节点
- 删除尾节点
图解:
示例代码:
/** * @brief: 删除数据 * @note: 先遍历链表,找到要删除的数据,再删除 * @param: head_node:头节点,data:要删除节点的数据 * @retval: 成功:返回0 * 失败:返回-1 * */ int dlink_list_DeleteListNode(node_p head_node,int data) { if(dlink_list_IsEmpty(head_node)) return -1; node_p tmp_p=NULL; node_p del_node=NULL; node_p last_node=NULL; node_p next_node=NULL; int flag=0; for(tmp_p=head_node;tmp_p->next_p!=NULL;tmp_p=tmp_p->next_p) { if(tmp_p->next_p->data==data) { del_node=tmp_p->next_p; last_node=tmp_p; next_node=tmp_p->next_p->next_p; flag=1; break; } } if(flag==0) { printf("要删除的数据不在链表中!!!!!\n"); return -1; } last_node->next_p=next_node; if (next_node!=NULL) next_node->prev_p=last_node; del_node->prev_p=NULL; del_node->next_p=NULL; free(del_node); return 0; }
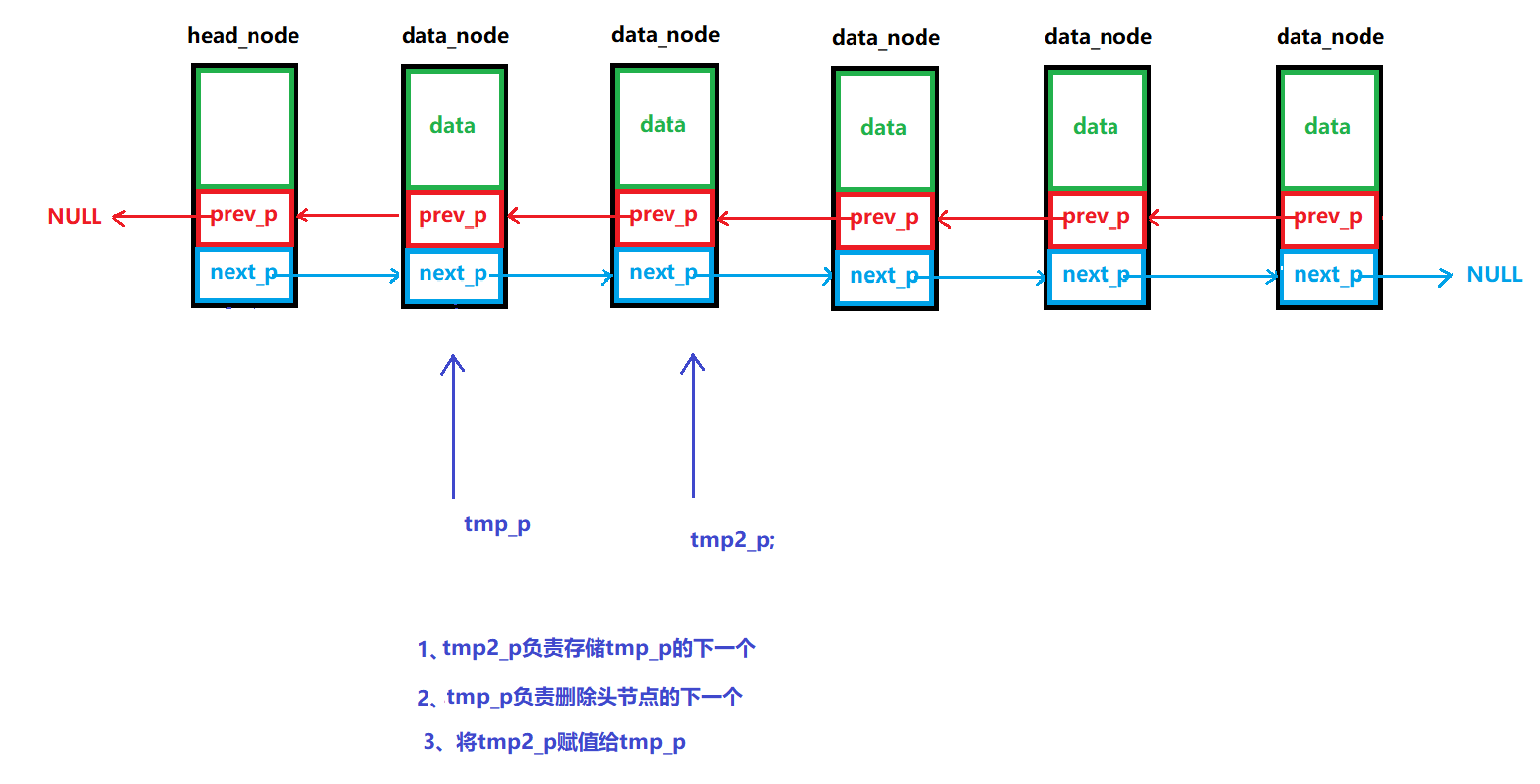
8、销毁链表
销毁链表是一个重要的内存管理操作,目的是释放链表占用的所有内存空间,防止内存泄漏。对于带头节点的双向链表,销毁过程需要遵循特定的顺序:
- 逐个删除数据节点:从头节点开始,依次删除每个数据节点
- 最后删除头节点:在所有数据节点都被删除后,最后删除头节点本身
- 重置指针:将相关指针设置为
NULL,避免悬空指针图解:
示例代码:
/** * @brief: 销毁链表 * @note: 先销毁数据节点,再销毁头节点 * @param: head_node:头节点 * @retval: none * */ void dlink_list_UnInit(node_p head_node) { if(dlink_list_IsEmpty(head_node)) { free(head_node); return; } node_p tmp_p=NULL; node_p tmp_p2=NULL; for(tmp_p=head_node->next_p;tmp_p!=NULL;tmp_p=tmp_p2) { tmp_p2=tmp_p->next_p; free(tmp_p); } free(head_node); }
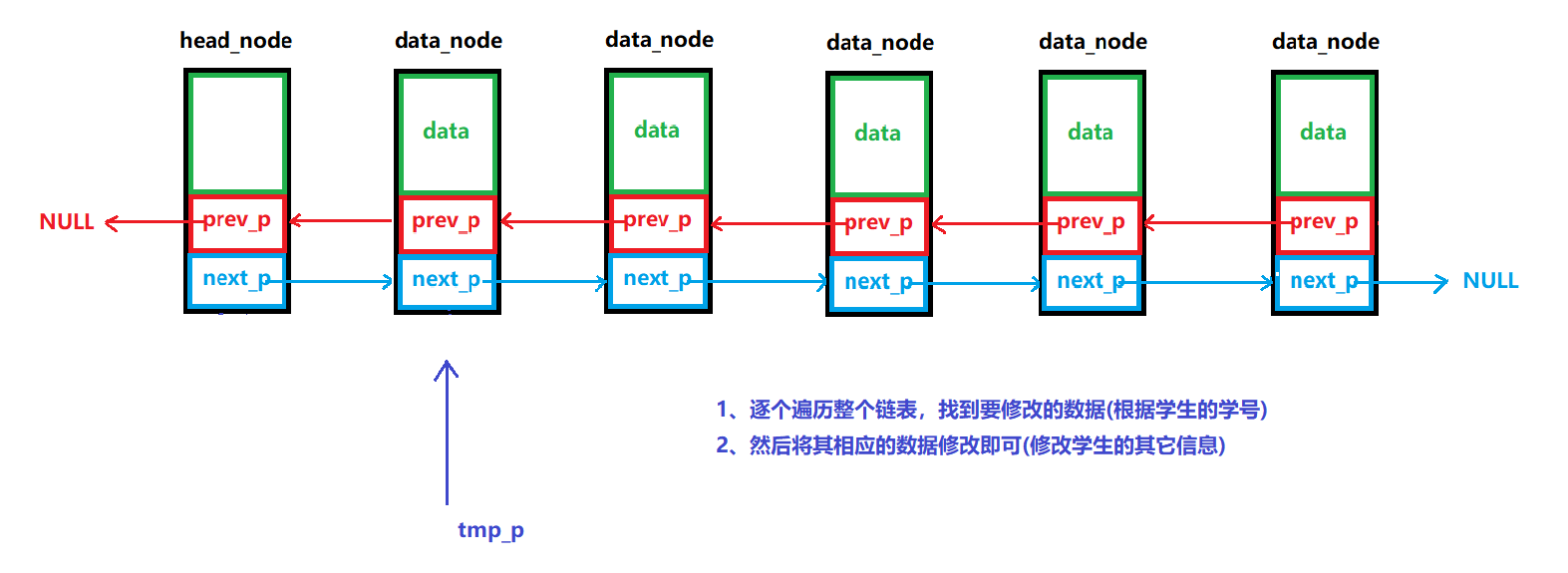
9、修改数据
修改链表中的数据是一个常见的操作,通常包括两个步骤:
- 查找节点:遍历链表,找到包含目标数据的节点
- 修改数据:直接修改该节点的
data字段值修改方式:
- 修改第一个匹配的节点:找到第一个包含目标数据的节点并修改
- 修改所有匹配的节点:遍历整个链表,修改所有包含目标数据的节点
图解:
示例代码:
/** * @brief: 修改数据 * @note: 先遍历链表,找到要修改的数据,再修改 * @param: head_node:头节点,data:要修改的数据,chang_data:修改后的数据 * @retval: 成功:返回0 * 失败:返回-1 * */ int dlink_list_ChangeNode(node_p head_node,int data,int chang_data) { if(dlink_list_IsEmpty(head_node)) return -1; node_p tmp_p=NULL; for(tmp_p=head_node->next_p;tmp_p!=NULL;tmp_p=tmp_p->next_p) { if(tmp_p->data==data) { tmp_p->data=chang_data; break; } } if(tmp_p==NULL) { printf("要修改的数据不在链表中!!!!!\n"); return -1; } return 0; }