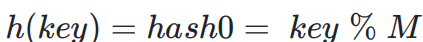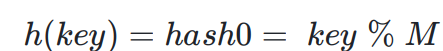C哈希表实现


【C++】哈希表实现
1. 哈希概念
哈希(hash)又称散列,是⼀种组织数据的方式。从译名来看,有散乱排列的意思。本质就是通过哈希 函数把关键字Key跟存储位置建立一个映射关系,查找时通过这个哈希函数计算出Key存储的位置,进行快速查找
1.1 直接定址法
当关键字的范围较集中时,直接定址法就是简单高效的方法,如⼀组关键字都在[0,99]之间, 那么开一个100个数的数组,每个关键字的值直接就是存储位置的下标。再如一组关键字值都在 [a,z]的小写字母,那么开一个26个数的数组,每个关键字acsii码-a 的ascii码就是存储位置的下标。 也就是说直接定址法本质就是用关键字计算出一个绝对位置或者相对位置
1.2 哈希冲突
两个不同的key可能会映射到同一个位置去,这种问题叫做哈希冲突, 或者哈希碰撞
1.3 负载因子
假设哈希表中已经映射存储了N个值,哈希表的大小为M,那么负载因子=N/M ,负载因子有些地方也翻译为载荷因子/装载因子等,负载因子越大,哈希冲突的概率越高,空间利用率越高;负载因子越小,哈希冲突的概率越低,空间利用率越低
1.4 哈希函数
一个好的哈希函数应该让N个关键字被等概率的均匀的散列分布到哈希表的M个空间中,但是实际中却很难做到,尽量往这个方向去考量设计
除法散列法/除留余数法
- 假设哈希表的大小为M,那么通过key除以M的余数作为映射位置的下标,也就是哈希函数为:h(key)=key%M
- 当使用除法散列法时,要尽量避免M为某些值,如2的幂,10的幂等
- 如果是2的幂,那么key % 2^x 本质相当于保留key的后X位,那么后x位相同的值,计算出的哈希值都是⼀样的,就冲突了。如果是10的幂 ,保留的都是 10进值的后x位
- 当使用除法散列法时,建议M取不太接近2的整数次幂的一个质数(素数)
1.5 处理哈希冲突
主要有两种两种方法,开放定址法和链地址法
1.5.1 开放定址法
在开放定址法中所有的元素都放到哈希表里,当一个关键字key用哈希函数计算出的位置冲突了,则按照某种规则找到一个没有存储数据的位置进行存储,开放定址法中负载因子一定是小于的。有三种:线性探测、⼆次探测、双重探测
1)线性探测
- 从发生冲突的位置开始,依次线性向后探测,直到寻找到下一个没有存储数据的位置为止,如果走到哈希表尾,则回绕到哈希表头的位置

- 线性探测的比较简单且容易实现,线性探测的问题假设,hash0位置连续冲突,hash0,hash1, hash2位置已经存储数据了,后续映射到hash0,hash1,hash2,hash3的值都会争夺hash3位 置,这种现象叫做群集/堆积。二次探测可以一定程度改善这个问题


2)二次探测
- 从发生冲突的位置开始,依次左右按二次方跳跃式探测,直到寻找到下一个没有存储数据的位置为 为,如果走到哈希表尾,则回绕到哈希表头的位置;如果往左走到哈希表头,则回绕到哈希表尾的位置

- 二次探测当hashi = (hash0 − i )%M 时,当hashi<0时,需要hashi+=M


1.5.2 开放定址法代码实现
哈希表结构
enum State
{
EXIST,
EMPTY,
DELETE
};
template<class K, class V>
struct HashData
{
pair<K, V> _kv;
State _state = EMPTY;
};
template<class K, class V>
class HashTable
{
private:
vector<HashData<K, V>> _tables;
size_t _n = 0; // 表中存储数据个数
};扩容
哈希表负载因子控制在0.7,当负载因子到0.7以后就需要扩容了,给了一个近似2倍的质数表,每次去质数表获取扩容后的大小
inline unsigned long __stl_next_prime(unsigned long n)
{
// Note: assumes long is at least 32 bits.
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
const unsigned long* first = __stl_prime_list;
const unsigned long* last = __stl_prime_list + __stl_num_primes;
const unsigned long* pos = lower_bound(first, last, n);
return pos == last ? *(last - 1) : *pos;
}key不能取模的问题
- 当key是string/Date等类型时,key不能取模,那么需要给HashTable增加一个仿函数,这个仿函数⽀持把key转换成一个可以取模的整形
- 自己实现一个仿函数传给这个参数,让不同的key转换出的整形值不同
- string 做哈希表的key很常见,可以考虑把string特化一下
template<class K>
class HashFunc
{
public:
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
class HashFunc<string>
{
public:
// 字符串转换成整形,可以把字符ascii码相加即可
// 但是直接相加的话,类似"abcd"和"bcad"这样的字符串计算出是相同的
// 这⾥我们使⽤BKDR哈希的思路,⽤上次的计算结果去乘以一个质数,这个质数一般去31, 131
等效果会⽐较好
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto ch : key)
{
hash += ch;
hash *= 131;
}
return hash;
}
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
private:
vector<HashData<K, V>> _tables;
size_t _n = 0; // 表中存储数据个数
};完整代码实现
1.5.3 链地址法
开放定址法中所有的元素都放到哈希表,链地址法中所有的数据不再直接存储在哈希表中,哈希表 中存储一个指针,没有数据映射这个位置时,这个指针为空,有多个数据映射到这个位置时,把这些冲突的数据链接成一个链表,挂在哈希表这个位置下面,链地址法也叫做拉链法或者哈希桶

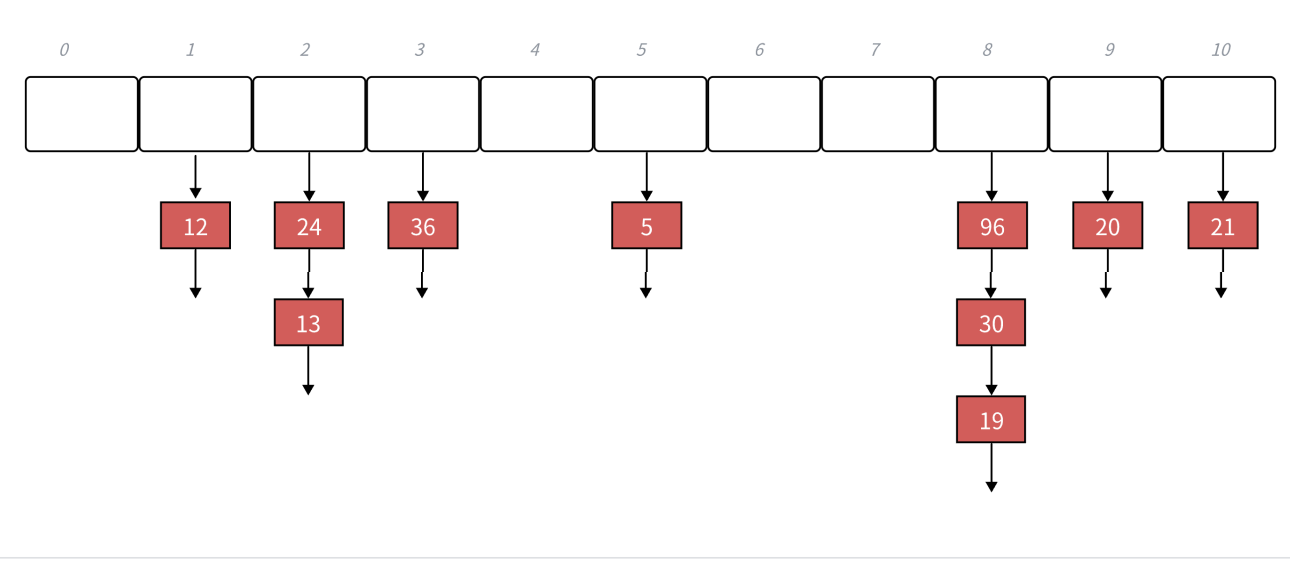
扩容
开放定址法负载因子必须小于1,链地址法的负载因子就没有限制了,可以大于1
这里大于1就扩容
插入逻辑
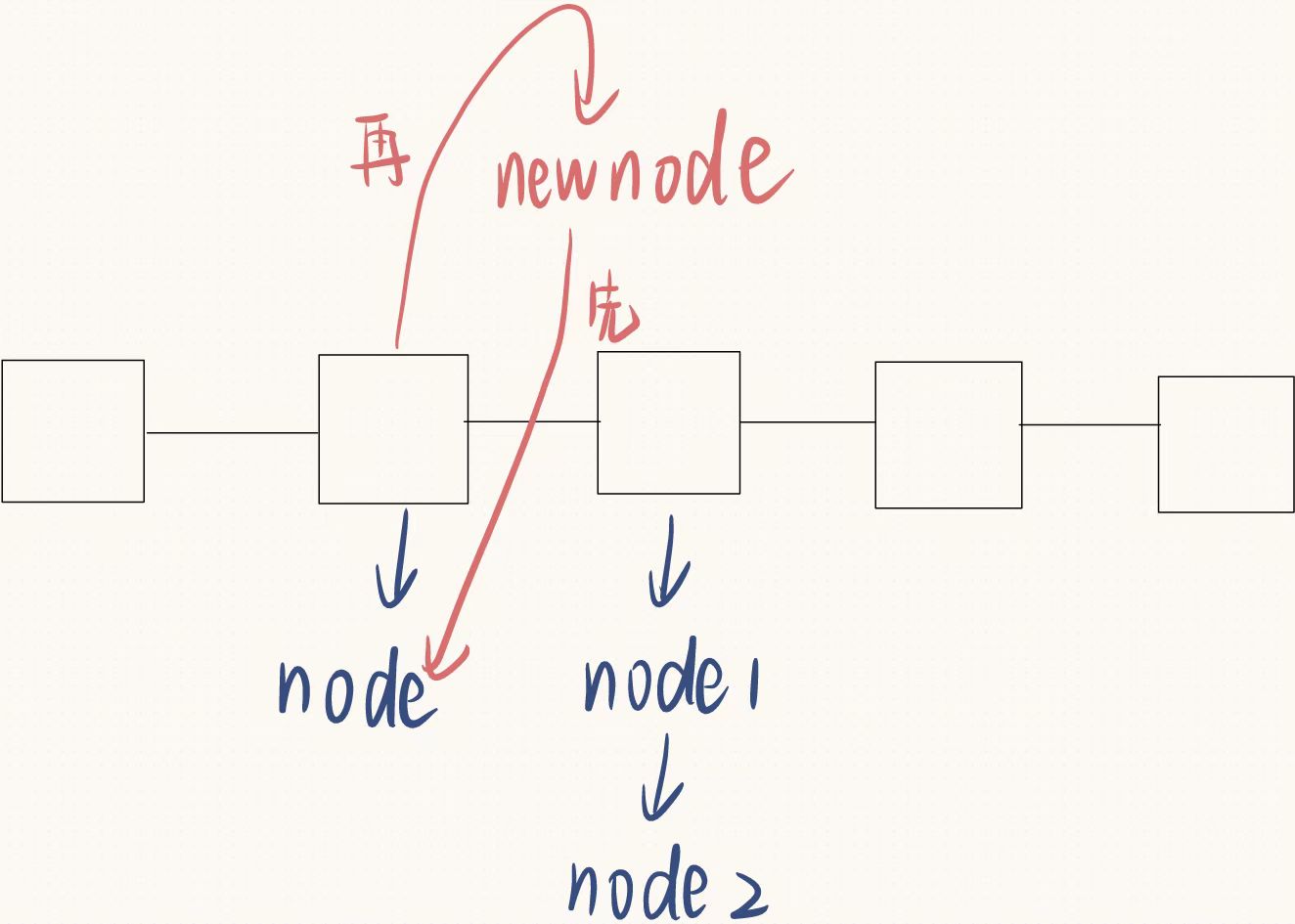
链地址法代码实现