深度学习残差网络ResNet与迁移学习
![读取图像(假设路径在csv第0列)img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 转为RGBimg = cv2.resize(img, (224, 224)) # 统一尺寸img = img.transpose((2, 0, 1)) # (H,W,C) → (C,H,W),适应PyTorchlabel = (label + 1) / 2 # 假设原始标签为[-1,1],归一化到[0,1]# 应用数据增强回归任务使用均方误差(MSE)损失# 前向传播。 https://bing.ee123.net/img/rand?artid=151264751](https://bing.ee123.net/img/rand?artid=151264751)

深度学习:残差网络ResNet与迁移学习
在卷积神经网络(CNN)的发展历程中,网络深度的增加曾被认为是提升模型性能的关键。然而,当网络深度超过一定限度后,会出现 梯度消失/爆炸和 退化问题,导致模型训练困难、性能不升反降。2015 年,何凯明等人提出的残差网络(ResNet)彻底打破了这一瓶颈,通过创新的残差结构和 Batch Normalization(BN)技术,成功训练出上千层的深层网络,不仅斩获当年 ImageNet 竞赛多项冠军,更成为后续深度学习模型设计的“基石”。本文将从 ResNet 的痛点出发,深入剖析其原理、结构,并结合 PyTorch 实现实战,带大家全面掌握这一经典网络。
一、ResNet 诞生的背景:深层 CNN 的两大“致命”问题
在 ResNet 出现之前,研究者们发现,当 CNN 的层数堆叠到一定程度(如超过 20 层),模型会出现两个难以解决的问题,直接限制了深层网络的应用。
1.1 梯度消失与梯度爆炸
神经网络的训练依赖反向传播:通过计算损失函数对各层参数的梯度,迭代更新权重。但在深层网络中,梯度会沿着网络层“反向传播”时逐渐放大或缩小,最终导致训练失效。
- 梯度消失:若每一层的梯度都小于 1(如激活函数使用 Sigmoid 时,导数最大值仅 0.25),经过多层传播后,梯度会呈指数级衰减,趋近于 0。此时,浅层网络的参数几乎无法更新,模型陷入“停滞”,ResNet 出现前的深层网络常因此训练失败。
- 梯度爆炸:若每一层的梯度都大于 1,反向传播时梯度会呈指数级增长,最终超出计算机的数值表示范围(如 NaN),导致训练崩溃。
传统解决方案(如参数初始化、使用 ReLU 激活函数)只能缓解浅层网络的问题,对深层网络(如 50 层以上)效果有限。
1.2 退化问题(Degradation)
除了梯度问题,深层网络还会出现“退化”:当网络层数增加时,训练误差和测试误差反而会上升,且这种上升并非由过拟合导致(过拟合仅表现为测试误差上升,训练误差下降)。
下图是论文中 20 层和 56 层 CNN 的性能对比:随着层数从 20 层增加到 56 层,训练误差和测试误差均显著上升,说明深层网络不仅没有学到更复杂的特征,反而丢失了浅层网络的学习能力。
退化问题的本质是:深层网络难以学习“恒等映射”(即让输入等于输出, H ( x )
x H(x) = x H(x)=x)。当某一层的最优映射就是恒等映射时,浅层网络可直接拟合,但深层网络需要通过复杂的参数调整来逼近这一简单映射,反而容易引入误差。
二、ResNet 的核心创新:残差结构与 Batch Normalization
为解决上述两大问题,ResNet 提出了两个关键设计:残差结构(Residual Block) 和 Batch Normalization(BN 层)。
2.1 残差结构:让网络“跳过”层,直接学习残差
ResNet 的核心思想是:**不要求深层网络直接学习复杂的映射 H ( x ) H(x) H(x),而是学习“残差” F ( x )
H ( x ) − x F(x) = H(x) - x F(x)=H(x)−x**。此时,原映射可表示为 H ( x )
F ( x ) + x H(x) = F(x) + x H(x)=F(x)+x,其中 x x x 是输入特征,通过“shortcut 连接”(捷径连接)直接传递到输出端,与 F ( x ) F(x) F(x) 相加。
这种结构的优势在于:
若最优映射是恒等映射( H ( x )
x H(x) = x H(x)=x),则网络只需让 F ( x )
0 F(x) = 0 F(x)=0 即可,无需复杂参数调整,从根本上解决了退化问题;- shortcut 连接直接传递梯度,避免了梯度在深层传播时的衰减,缓解了梯度消失问题。
2.1.1 残差结构的两种形式
根据输入输出特征图的维度是否一致,残差结构分为 恒等映射(Identity Mapping) 和 维度匹配(Dimensionality Matching) 两种:
| 类型 | 适用场景 | 结构特点 |
|---|---|---|
| 恒等映射 | 输入、输出特征图的通道数、尺寸完全一致(如同一阶段的残差块) | shortcut 连接直接传递 x x x,无需额外参数 |
| 维度匹配 | 输入、输出特征图的通道数或尺寸不同(如不同阶段的过渡) | shortcut 连接需通过 1 × 1 1×1 1×1 卷积调整 x x x 的维度,确保 F ( x ) F(x) F(x) 与 x x x 可相加 |
两种结构的示意图如下: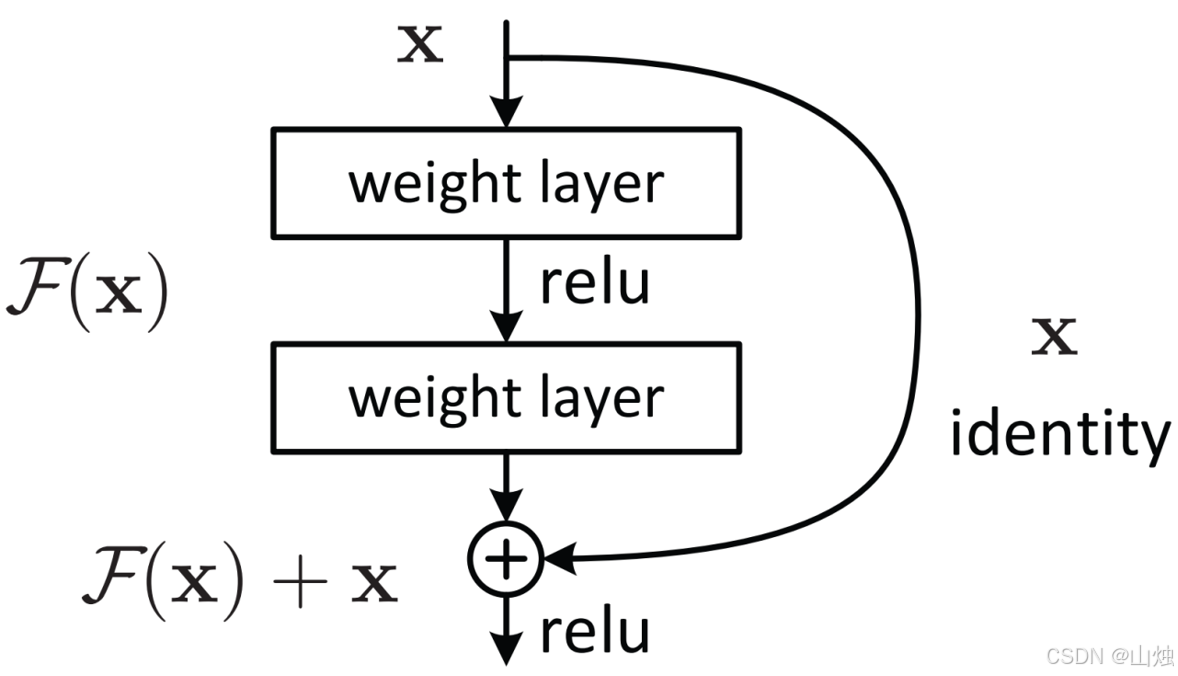
以常用的 3 × 3 3×3 3×3 卷积残差块为例,恒等映射的计算流程为:
- 输入 x x x 经过第一个 3 × 3 3×3 3×3 卷积层,激活函数为 ReLU;
- 经过第二个 3 × 3 3×3 3×3 卷积层(无激活);
- 通过 shortcut 连接将原始输入 x x x 与第二步的输出相加;
- 最后经过 ReLU 激活,得到残差块的输出。
2.2 Batch Normalization(BN 层):解决梯度消失
为进一步缓解梯度消失问题,ResNet 引入了 Batch Normalization(批量归一化) 技术,其核心作用是:对每一层的输入特征进行归一化,使特征分布满足“均值为 0、方差为 1”,避免因特征值过大或过小导致梯度消失。
2.2.1 BN 层的工作原理
BN 层通常插入在卷积层之后、激活函数之前,具体步骤如下:
计算批次均值和方差:对当前批次(Batch)的特征图,计算每个通道的均值 μ \mu μ 和方差 σ 2 \sigma^2 σ2;
归一化:将特征图的每个元素减去均值、除以标准差(加 ϵ \epsilon ϵ 避免分母为 0),得到归一化后的特征 x ^
x − μ σ 2 + ϵ \hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} x^=σ2+ϵ
x−μ;
缩放与偏移:引入可学习参数 γ \gamma γ(缩放因子)和 β \beta β(偏移因子),对归一化后的特征进行调整: y
γ ⋅ x ^ + β y = \gamma \cdot \hat{x} + \beta y=γ⋅x^+β,确保网络可自主学习最优的特征分布。
2.2.2 BN 层的优势
- 加速训练收敛:归一化后的特征分布更稳定,可使用更大的学习率;
- 缓解梯度消失:避免特征值过大导致激活函数进入饱和区(如 Sigmoid);
- 降低过拟合:批次内的随机归一化相当于一种轻微的数据增强。
三、ResNet 的网络结构:从 18 层到 152 层的演变
ResNet 通过堆叠残差块形成不同深度的网络,常见的有 ResNet-18、ResNet-34、ResNet-50、ResNet-101、ResNet-152 等。其核心区别在于残差块的类型和数量:
- 浅层 ResNet(18/34 层):使用2 个 3 × 3 3×3 3×3 卷积组成的残差块(Basic Block);
- 深层 ResNet(50/101/152 层):使用** 1 × 1 + 3 × 3 + 1 × 1 1×1 + 3×3 + 1×1 1×1+3×3+1×1 卷积组成的残差块(Bottleneck Block)**,减少参数数量和计算量。
3.1 ResNet 的整体结构
以 ResNet-50 为例,网络分为 5 个阶段(conv1 ~ conv5_x),每个阶段由多个残差块组成,最后通过全局平均池化和全连接层输出分类结果。具体结构如下表:
| 阶段 | 层类型 | 输出尺寸 | 残差块数量 | 卷积核参数 |
|---|---|---|---|---|
| conv1 | 7×7 卷积 + BN + ReLU | 112×112×64 | - | 7×7, 64, stride=2 |
| - | 3×3 最大池化 | 56×56×64 | - | stride=2 |
| conv2_x | Bottleneck Block | 56×56×256 | 3 | 1×1(64) → 3×3(64) → 1×1(256) |
| conv3_x | Bottleneck Block | 28×28×512 | 4 | 1×1(128) → 3×3(128) → 1×1(512) |
| conv4_x | Bottleneck Block | 14×14×1024 | 6 | 1×1(256) → 3×3(256) → 1×1(1024) |
| conv5_x | Bottleneck Block | 7×7×2048 | 3 | 1×1(512) → 3×3(512) → 1×1(2048) |
| - | 全局平均池化 | 1×1×2048 | - | - |
| fc | 全连接层 | 1×1×1000 | - | 2048 → 1000(ImageNet 分类) |
注:stride=2 的卷积层用于缩小特征图尺寸, 1 × 1 1×1 1×1 卷积用于调整通道数(维度匹配)。
3.2 不同深度 ResNet 的对比
不同深度的 ResNet 在参数数量、计算量(FLOPs)和性能上存在差异,实际应用中需根据任务需求选择:
| 网络型号 | 残差块类型 | 总层数 | 参数数量(M) | FLOPs( 1 0 9 10^9 109) | ImageNet Top-1 准确率 |
|---|---|---|---|---|---|
| ResNet-18 | Basic Block | 18 | 11.7 | 1.8 | 69.76% |
| ResNet-34 | Basic Block | 34 | 21.8 | 3.6 | 73.31% |
| ResNet-50 | Bottleneck Block | 50 | 25.6 | 3.8 | 76.13% |
| ResNet-101 | Bottleneck Block | 101 | 44.5 | 7.6 | 77.37% |
| ResNet-152 | Bottleneck Block | 152 | 60.2 | 11.3 | 78.31% |
可以看出:随着深度增加,ResNet 的准确率逐渐提升,但参数数量和计算量也随之增长。因此,在资源有限的场景(如移动端),ResNet-18/34 更合适;而在追求高准确率的场景(如服务器端图像分类),可选择 ResNet-50/101。
四、ResNet 实战:PyTorch 实现与迁移学习
ResNet 不仅是经典的网络结构,更是迁移学习的“利器”。PyTorch 的 torchvision.models 库提供了预训练的 ResNet 模型,可直接用于新任务的微调。下面以“人脸关键点预测”(回归任务)为例,演示 ResNet 的实现与迁移学习。
4.1 任务背景
人脸关键点预测是典型的回归任务:输入一张人脸图像,输出 68 个关键点的坐标(共 136 个数值,每个关键点含 x、y 坐标)。由于数据集通常较小,直接训练深层网络易过拟合,因此采用迁移学习:基于预训练的 ResNet-18,微调全连接层以适应回归任务。
4.2 实现步骤
步骤 1:导入依赖库
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from torchvision import models, transforms
import pandas as pd
import cv2步骤 2:定义数据集类(人脸关键点数据集)
假设数据集包含图像路径和对应的关键点坐标(标签已归一化到 0~1):
class FaceKeyPointDataset(Dataset):
def __init__(self, csv_file, root_dir, transform=None):
self.key_pts_frame = pd.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.key_pts_frame)
def __getitem__(self, idx):
# 读取图像(假设路径在csv第0列)
img_name = os.path.join(self.root_dir, self.key_pts_frame.iloc[idx, 0])
img = cv2.imread(img_name)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 转为RGB
img = cv2.resize(img, (224, 224)) # 统一尺寸
img = img.transpose((2, 0, 1)) # (H,W,C) → (C,H,W),适应PyTorch
label = self.key_pts_frame.iloc[idx, 1:].values.astype('float')
label = (label + 1) / 2 # 假设原始标签为[-1,1],归一化到[0,1]
label = torch.tensor(label, dtype=torch.float32)
# 应用数据增强
if self.transform:
img = self.transform(img)
return img, label步骤 3:加载预训练 ResNet,修改全连接层
预训练的 ResNet-18 默认输出 1000 类(ImageNet 分类),需将最后一层全连接层改为输出 136 个值(回归任务):
class ResNetKeyPointModel(nn.Module):
def __init__(self, pretrained=True):
super(ResNetKeyPointModel, self).__init__()
self.resnet = models.resnet18(pretrained=pretrained)
# 修改最后一层全连接层
self.resnet.fc = nn.Linear(self.resnet.fc.in_features, 136) # 回归136个关键点
self.sigmoid = nn.Sigmoid() # 确保输出在[0,1]
def forward(self, x):
x = self.resnet(x)
x = self.sigmoid(x)
return x步骤 4:数据预处理与加载
# 数据增强与预处理
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
# 加载数据集
train_dataset = FaceKeyPointDataset(csv_path="train.csv", root_dir="data", transform=transform)
test_dataset = FaceKeyPointDataset(csv_path="test.csv", root_dir="data", transform=transform)
# 数据加载器
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)步骤 5:定义训练与评估函数
回归任务使用均方误差(MSE)损失,优化器用 Adam:
def train_model(model, train_loader, criterion, optimizer, epochs=5):
model = model.to(device) # device = "cuda" if torch.cuda.is_available() else "cpu"
for epoch in range(epochs):
running_loss = 0.0
for i, (images, labels) in enumerate(train_loader):
images, labels = images.to(device), labels.to(device)
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 反向传播与优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item() * images.size(0)
# 打印 epoch 损失
epoch_loss = running_loss / len(train_loader.dataset)
print(f"Epoch {epoch+1}/{epochs}, Loss: {epoch_loss:.4f}")
# 评估模型
test_loss = evaluate_model(model, test_loader, criterion)
print(f"Epoch {epoch+1}/{epochs}, Test Loss: {test_loss:.4f}")
def evaluate_model(model, test_loader, criterion):
model = model.to(device)
model.eval()
total_loss = 0.0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device)
outputs = model
odel.to(device)
model.eval()
total_loss = 0.0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device)
outputs = model