【LeetCode热题100道笔记+动画】完全平方数

题目描述

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：
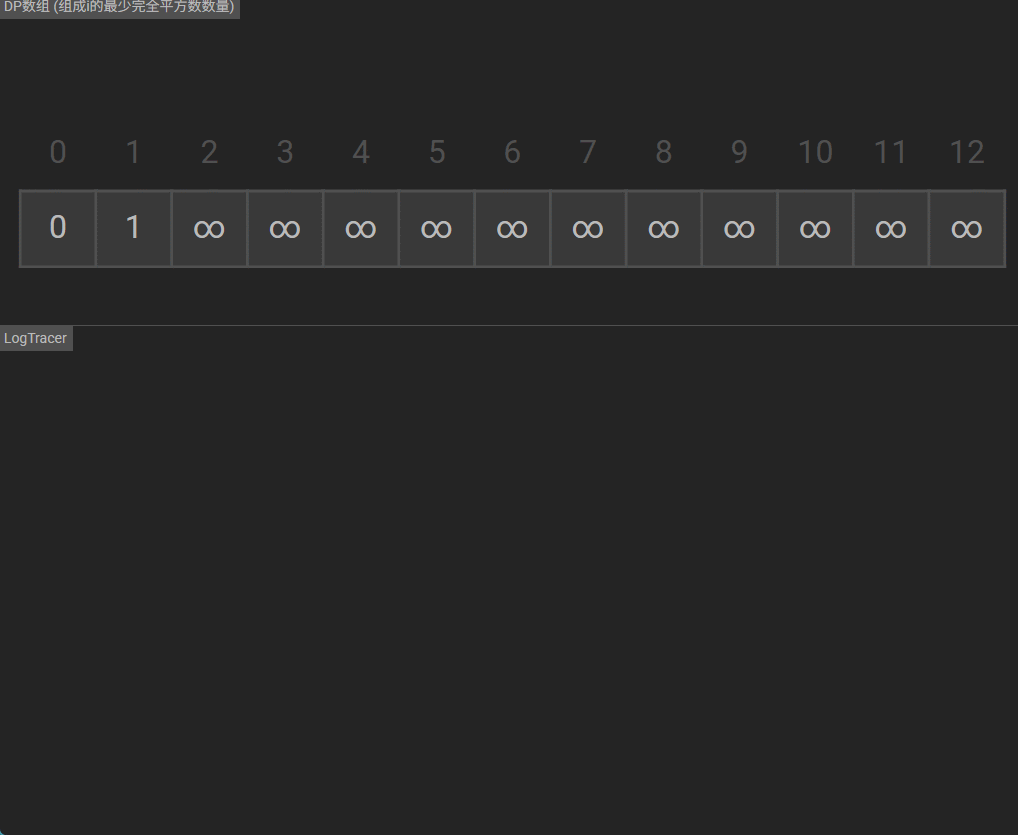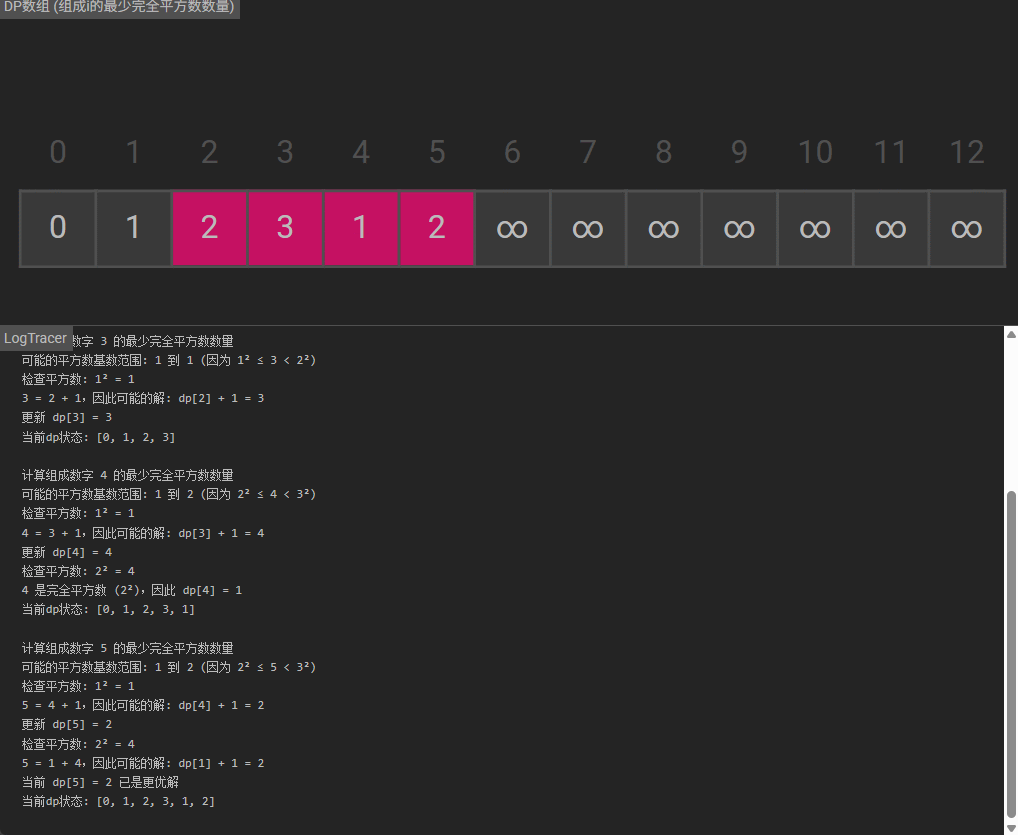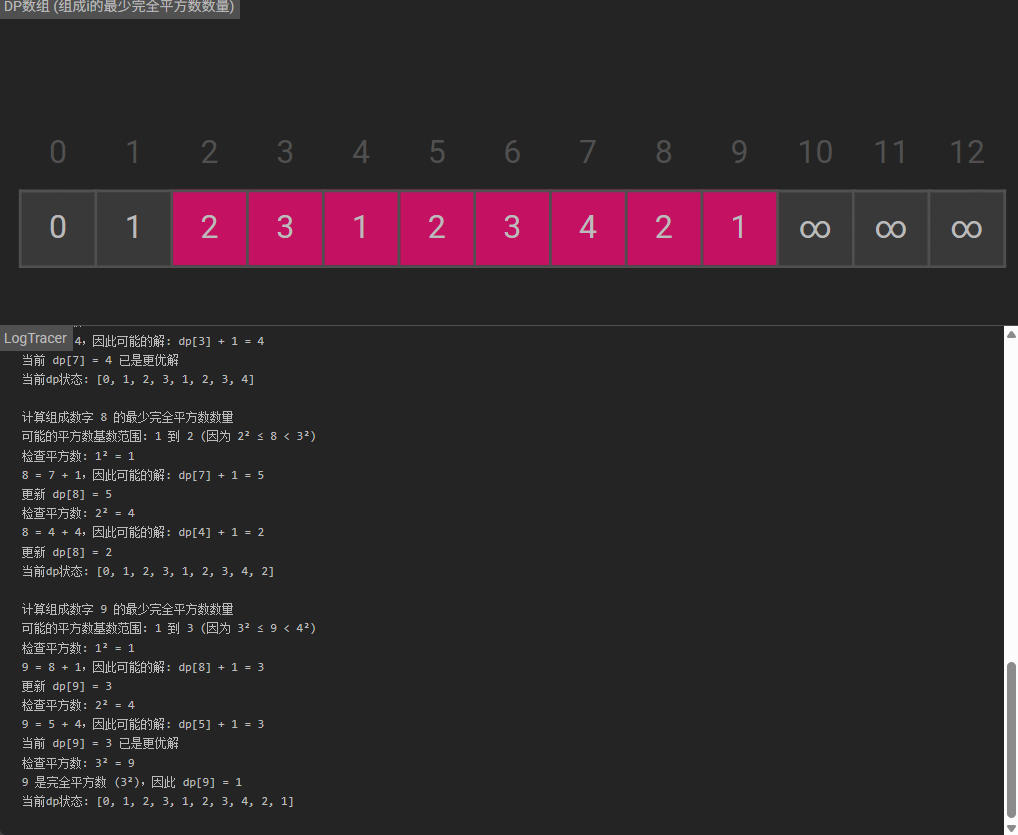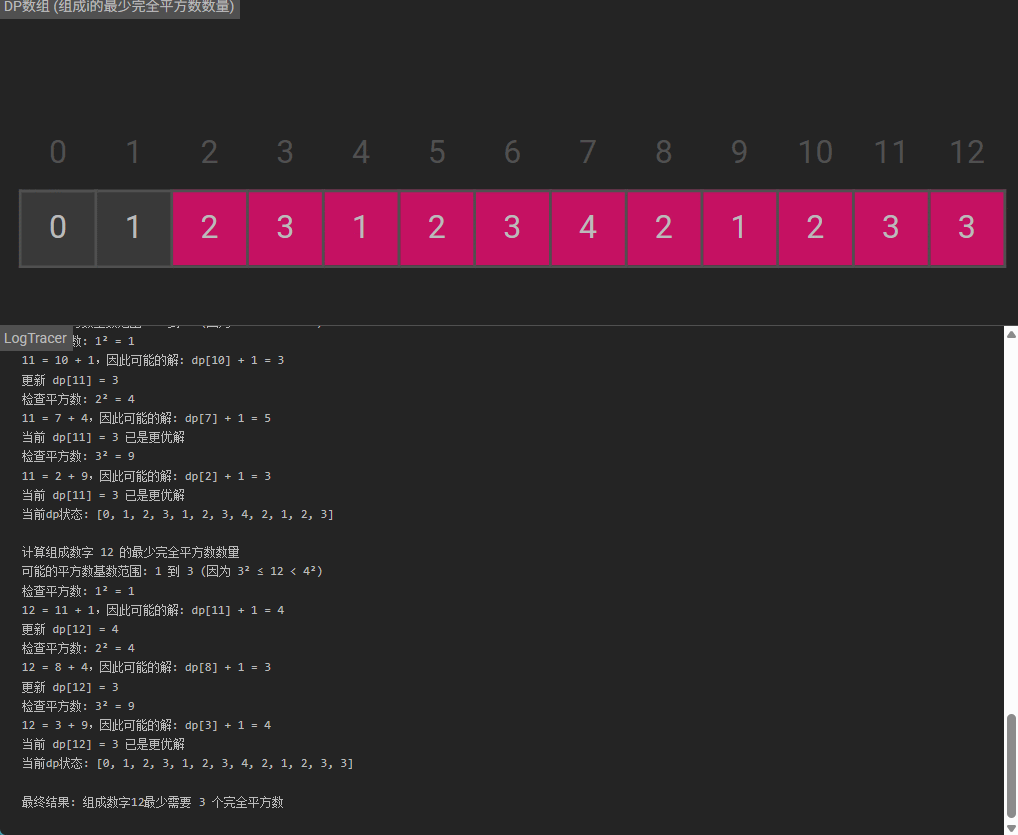
输入：n = 12
输出：3
解释：12 = 4 + 4 + 4

示例 2：
输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

• 1<=n<=1041 <= n <= 10^41<=n<=104

思考

将问题转化为完全背包问题：完全平方数视为物品（面值为1², 2², …, ⌊√n⌋²），目标是用最少物品数凑成总和n。通过动态规划追踪每个数的最少完全平方数组成数量。

算法过程

1. 初始化：

   • dp[i] 表示组成数 i 所需的最少完全平方数数量
   • 数组初始化为 Infinity（标记未计算状态）
   • 特例：dp[0] = 0（辅助状态，0由0个平方数组成），dp[1] = 1（1=1²）

2. 状态更新：

   • 遍历每个数 i（从2到n）：
     • 计算最大平方数基数 top = ⌊√i⌋（平方数不超过i）
     • 遍历所有可能的平方数 j²（j从1到top）：
       • 若 i = j²，则 dp[i] = 1（自身就是完全平方数）
       • 否则，dp[i] = min(dp[i], dp[i - j²] + 1)（基于 i-j² 的解加1个平方数j²）

3. 返回结果：dp[n] 即为组成n的最少完全平方数数量

时间复杂度

• 时间复杂度：O(n√n)，外层遍历n个数，内层遍历每个数对应的√i个平方数
• 空间复杂度：O(n)，需存储长度为n+1的dp数组

该方法通过完全背包思路，高效求解最少平方数组合，利用数学特性（限制j的范围为1到⌊√i⌋）减少无效计算。

代码

/**
 * @param {number} n
 * @return {number}
 */
var numSquares = function(n) {
    const dp = Array(n+1).fill(Infinity);
    dp[1] = 1;

    for (let i = 2; i <= n; i++) {
        const top = Math.floor(Math.sqrt(i));
        for (let j = 1; j <= top; j++) {
            if (i > j * j) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            } else if (i === j * j) {
                dp[i] = 1;
            }
        }
    }    

    return dp[n];    
};

可视化