基于Basilisk库实现地面目标定向


基于Basilisk库实现地面目标定向
一、背景介绍
航天器姿态对地面目标定向控制在现代空间技术中具有重要的科学价值和工程意义。这一技术是实现精确对地观测、通信中继、以及空间资源开发的核心基础。
从科学研究角度而言,精确的地面目标定向能力是地球科学、气候监测、以及环境变化研究的关键技术支撑。通过高精度姿态控制,遥感卫星能够实现亚米级的地面分辨率,为全球变化监测、灾害评估、以及资源勘探提供高质量的观测数据。特别是在气候变化研究钟,长期稳定的观测几何关系对于数据的时序一致性和科学可信度至关重要。
在工程应用层面,地面目标定向技术直接决定了航天任务的成败。对于商业遥感卫星而言,指向经度直接影响图像质量和商业价值;对于通信卫星,精确的地面站跟踪能力是保证通信链路稳定性的前提;对于军用侦察卫星,快速准确的目标捕获和跟踪能力更是核心战术优势。现代航天器通常要求指向精度达到角秒级别,这对姿态控制系统提出了极高的技术挑战。
从控制理论角度分析,地面目标定向问题本质上是一个时变参考跟踪控制问题。由于航天器轨道运动的周期性特征,地面目标在航天器体坐标系中呈现复杂的时变运动轨迹,这要求姿态控制系统具备良好的动态响应特性和鲁棒性。此外,地面目标的可见性约束(如仰角限制、遮挡条件)使得控制问题具有约束优化的特征,需要在满足物理约束的前提下实现最优控制性能。
从技术实现方面,现代航天器通常采用反作用轮、控制力矩陀螺等执行机构,结合星敏感器、惯性测量单元等高精度传感器,构建闭环姿态控制系统。其中,MRP等现代姿态表示方法的应用,有效避免了传统欧拉角的奇点问题,提高了控制算法的数值稳定性。同时考虑到航天器的功耗限制和执行机构的饱和约束,控制算法设计需要在控制精度和能源消耗之间寻求平衡。
二、仿真框架
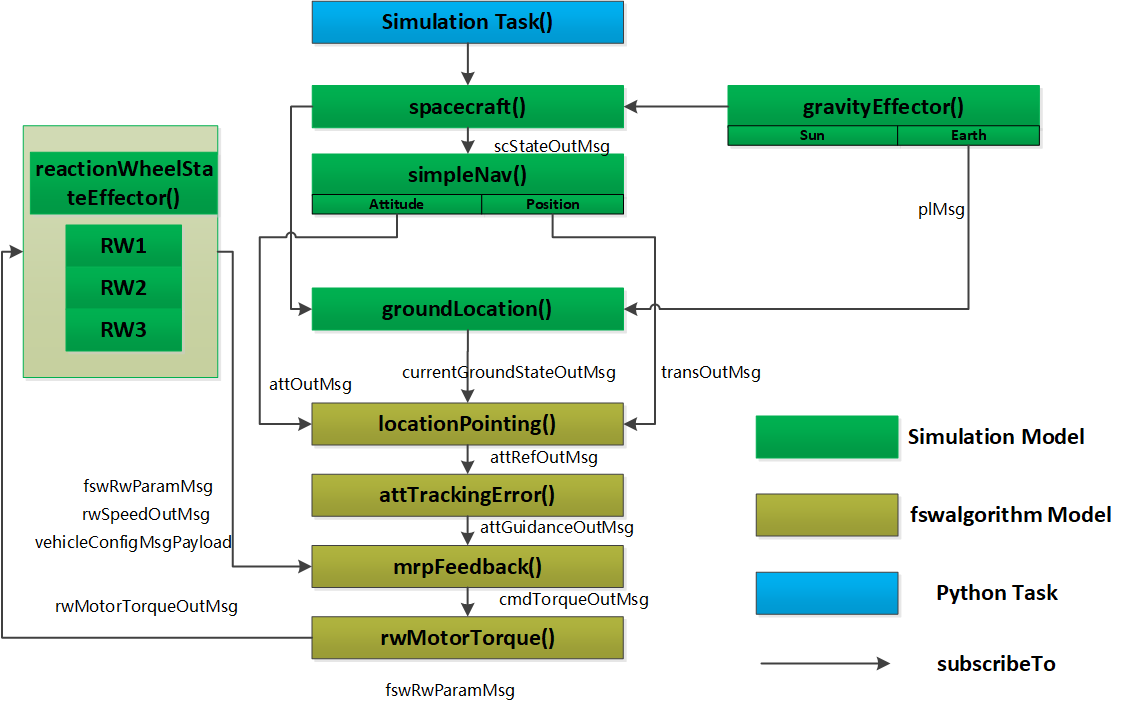
在Basilisk库中实现对地面目标定向的核心是locationPoint,通常应用的场景是在过顶目标上空时,下传数据给地面站等,这里仅从信号的角度出发,给出“信号链->控制链->调度与验证”的最小闭环。
(1)环境/导航
行星与动力学:gravFactory.createEarth+spiceInterface(UTC)->作为中央天体;spacecraft载入惯量与轨道初始状态,加入动力学。
导航:simpleNav.scStateInMsg->spacecraft.scStateOutMsg;输出attOutMsg、transOutMsg(姿态/位置速度)
(2)目标几何与可见性
groundLocation:设置planetRadius、经纬高、minimumElevation。输出地面站与目标的可见性。
(3)制导(参考姿态生成)
locationPointing:设指向轴pHat_B=[0,0,1]
scAttInMsg->simpleNav.attOutMsg
scTransInMsg->simpleNav.transOutMsg
locationInMsg->groundLocation.currentGroundStateOutMsg
(4)跟踪误差与控制
attTrackingError:
attRefInMsg->locationPointing.attRefOutMsg
attNavInMsg->simpleNav.attOutMsg
输出attGuidOutMsg
mrpFeedback(PD律)
(5)力矩分配与执行
rwMotorTorque:controlAxes_B,rwParamsInMsg,vehControlInMsg,输出为rwMotorTorqueOutMsg
(6)调度与优先级
simpleNav->groundLocation->locationPointing->attTrackingError->mrpFeedback->rwMotorTorque/ReactionWheels。
三、仿真结果
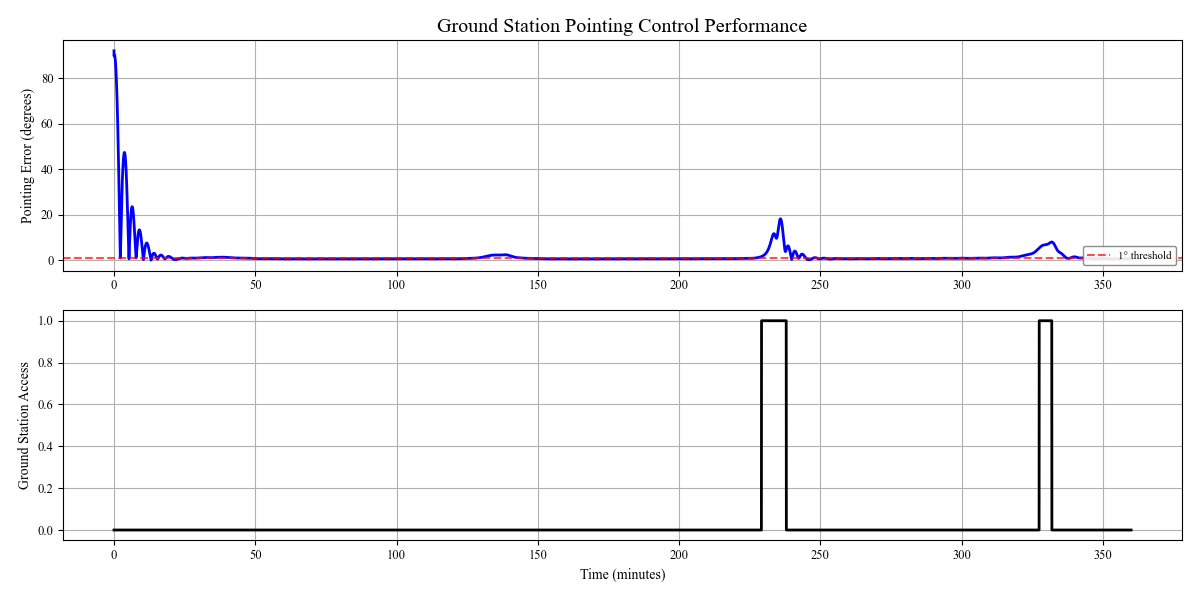
结果显示,姿态对地定向在轨一昼夜内总体稳定:在进入任务初段与两段可见窗口内出现可解释的瞬时误差峰,其余时段主角误差基本维持在1°阈值之下。误差尖峰对应参考视线角速度骤增与参考切换(由“非可见”转入“可见”)的双重效应

系统以较小阻尼快速收敛。反作用轮状态图表明,三轮转速呈明显的轨道频率与高频叠加起伏,初始捕获阶段与可见窗口边缘存在尖峰;而机体控制力矩长期接近零均值,仅在参考快速变化时出现短时脉冲。这一“力矩小而轮速仍变”的现象来自执行机构“积分”特性与周期性外扰(重力梯度、气动、光压)共同作用:微小的有符号力矩被累积为轮动量的往复变化,且在斜距较小、横向相对速度较大时(地面站附近通过)需求力矩增大,驱动轮速尖峰。总体而言,所选PD增益与轮力矩上限在当前任务几何下可实现“可见期间快速捕获、非可见期间低能量维持”的折衷。
四、源码
"""
简化的地面站指向仿真
基于locationPointing->attTrackingError->mrpFeedback的控制链路
"""
import numpy as np
import matplotlib.pyplot as plt
import os
from Basilisk.fswAlgorithms import locationPointing, attTrackingError, mrpFeedback, rwMotorTorque
from Basilisk.utilities import macros as mc
from Basilisk.utilities import SimulationBaseClass, unitTestSupport, orbitalMotion, simIncludeGravBody, simIncludeRW
from Basilisk.architecture import astroConstants as AC, messaging
from Basilisk.simulation import (spacecraft, simpleNav, groundLocation,
reactionWheelStateEffector)
def run_ground_pointing(sim_hours: float = 2.0):
"""
简化的地面站指向仿真
Args:
sim_hours: 仿真时长(小时)
"""
# 1) 仿真容器与时间
sim = SimulationBaseClass.SimBaseClass()
proc = sim.CreateNewProcess("groundPointProc")
dt = mc.sec2nano(1.0)
proc.addTask(sim.CreateNewTask("groundPointTask", dt))
# 2) 地球 + SPICE(绝对历元)
grav = simIncludeGravBody.gravBodyFactory()
earth = grav.createEarth()
earth.isCentralBody = True
mu = earth.mu
spice = grav.createSpiceInterface(time="2020 JAN 01 12:00:00 (UTC)")
sim.AddModelToTask("groundPointTask", spice, -1)
plMsg = spice.planetStateOutMsgs[0] # 地球
# 添加地球重力模型
basiliskPath = os.path.dirname(os.path.abspath(__file__))
dataFile = os.path.join(basiliskPath, '..', 'supportData', 'LocalGravData', 'GGM03S.txt')
if os.path.exists(dataFile):
earth.useSphericalHarmonicsGravityModel(dataFile, 8)
# 3) 航天器
sc = spacecraft.Spacecraft()
sc.ModelTag = "spacecraft"
sim.AddModelToTask("groundPointTask", sc, 1)
# 轨道参数:太阳同步轨道
oe = orbitalMotion.ClassicElements()
oe.a = 7028.14e3 # 半长轴 (m)
oe.e = 0.0 # 偏心率
oe.i = np.deg2rad(97.991) # 倾角 (rad)
oe.Omega = np.deg2rad(272.366) # 升交点赤经 (rad)
oe.omega = 0.0 # 近地点幅角 (rad)
oe.f = 0.0 # 真近点角 (rad)
rN, vN = orbitalMotion.elem2rv(mu, oe)
sc.hub.r_CN_NInit = rN
sc.hub.v_CN_NInit = vN
sc.hub.sigma_BNInit = [[0.1], [0.05], [-0.1]] # 初始姿态误差
sc.hub.omega_BN_BInit = [[0.001], [-0.001], [0.002]] # 初始角速度
# 航天器惯量
I = [900., 0., 0.,
0., 800., 0.,
0., 0., 600.]
sc.hub.IHubPntBc_B = unitTestSupport.np2EigenMatrix3d(I)
grav.addBodiesTo(sc)
# 4) 导航 - 高优先级,确保首先执行
sNav = simpleNav.SimpleNav()
sNav.ModelTag = "simpleNav"
sNav.scStateInMsg.subscribeTo(sc.scStateOutMsg)
sim.AddModelToTask("groundPointTask", sNav, 100) # 高优先级
# 5) 地面站目标(北京:40°N, 116°E)
target = groundLocation.GroundLocation()
target.ModelTag = "groundTarget"
target.planetRadius = AC.REQ_EARTH * 1e3 # 地球半径
target.specifyLocation(np.deg2rad(40.0), np.deg2rad(116.0), 0.0) # 纬度、经度、高度
target.minimumElevation = np.deg2rad(10.0) # 最小仰角10度
target.maximumRange = 1e12 # 最大距离(实际上不限制)
target.addSpacecraftToModel(sc.scStateOutMsg)
target.planetInMsg.subscribeTo(plMsg)
sim.AddModelToTask("groundPointTask", target, 90)
# 6) 位置指向控制器 - 使Z轴指向地面目标
locPointing = locationPointing.locationPointing()
locPointing.ModelTag = "locationPointing"
locPointing.pHat_B = [0.0, 0.0, 1.0] # Z轴(载荷轴)指向目标
locPointing.scAttInMsg.subscribeTo(sNav.attOutMsg)
locPointing.scTransInMsg.subscribeTo(sNav.transOutMsg)
locPointing.locationInMsg.subscribeTo(target.currentGroundStateOutMsg)
sim.AddModelToTask("groundPointTask", locPointing, 80)
# 7) 姿态跟踪误差计算
trackingError = attTrackingError.attTrackingError()
trackingError.ModelTag = "attTrackingError"
trackingError.attRefInMsg.subscribeTo(locPointing.attRefOutMsg) # 目标姿态参考
trackingError.attNavInMsg.subscribeTo(sNav.attOutMsg) # 当前姿态
sim.AddModelToTask("groundPointTask", trackingError, 70)
# 8) MRP反馈控制器
mrpControl = mrpFeedback.mrpFeedback()
mrpControl.ModelTag = "mrpFeedback"
mrpControl.guidInMsg.subscribeTo(trackingError.attGuidOutMsg) # 从跟踪误差获取控制指令
mrpControl.K = 1.5 # 保守的比例增益
mrpControl.P = 8.0 # 保守的微分增益
mrpControl.Ki = 0.0 # 无积分增益
sim.AddModelToTask("groundPointTask", mrpControl, 60)
# 9) 反作用轮系统
# 创建3个正交反作用轮
rwFactory = simIncludeRW.rwFactory()
varRWModel = messaging.BalancedWheels
for axis in [[1,0,0], [0,1,0], [0,0,1]]:
rwFactory.create("Honeywell_HR16", axis,
maxMomentum=50., Omega=100., # RPM
RWModel=varRWModel,
useMaxTorque=True) # 启用力矩限制
# 反作用轮状态效应器
numRW = rwFactory.getNumOfDevices()
rwStateEffector = reactionWheelStateEffector.ReactionWheelStateEffector()
rwStateEffector.ModelTag = "RW_StateEffector"
rwFactory.addToSpacecraft(sc.ModelTag, rwStateEffector, sc)
sim.AddModelToTask("groundPointTask", rwStateEffector)
# 反作用轮力矩映射
rwMotorTorqueObj = rwMotorTorque.rwMotorTorque()
rwMotorTorqueObj.ModelTag = "rwMotorTorque"
rwMotorTorqueObj.controlAxes_B = [1,0,0,0,1,0,0,0,1] # 3x3单位矩阵
fswRwParamMsg = rwFactory.getConfigMessage()
rwMotorTorqueObj.rwParamsInMsg.subscribeTo(fswRwParamMsg)
rwMotorTorqueObj.vehControlInMsg.subscribeTo(mrpControl.cmdTorqueOutMsg)
rwStateEffector.rwMotorCmdInMsg.subscribeTo(rwMotorTorqueObj.rwMotorTorqueOutMsg)
sim.AddModelToTask("groundPointTask", rwMotorTorqueObj)
# 10) 航天器配置消息
vehicleConfigOut = messaging.VehicleConfigMsgPayload()
vehicleConfigOut.ISCPntB_B = I
configDataMsg = messaging.VehicleConfigMsg().write(vehicleConfigOut)
mrpControl.rwParamsInMsg.subscribeTo(fswRwParamMsg)
mrpControl.rwSpeedsInMsg.subscribeTo(rwStateEffector.rwSpeedOutMsg)
mrpControl.vehConfigInMsg.subscribeTo(configDataMsg)
# 11) 数据记录器
locLog = locPointing.attRefOutMsg.recorder()
trackLog = trackingError.attGuidOutMsg.recorder()
navAttLog = sNav.attOutMsg.recorder()
navTransLog = sNav.transOutMsg.recorder()
rwSpeedLog = rwStateEffector.rwSpeedOutMsg.recorder()
mrpTorqueLog = mrpControl.cmdTorqueOutMsg.recorder()
accessLog = target.accessOutMsgs[-1].recorder()
groundStateLog = target.currentGroundStateOutMsg.recorder()
sim.AddModelToTask("groundPointTask", locLog)
sim.AddModelToTask("groundPointTask", trackLog)
sim.AddModelToTask("groundPointTask", navAttLog)
sim.AddModelToTask("groundPointTask", navTransLog)
sim.AddModelToTask("groundPointTask", rwSpeedLog)
sim.AddModelToTask("groundPointTask", mrpTorqueLog)
sim.AddModelToTask("groundPointTask", accessLog)
sim.AddModelToTask("groundPointTask", groundStateLog)
# 12) 运行仿真
sim.InitializeSimulation()
sim.ConfigureStopTime(mc.hour2nano(sim_hours))
sim.ExecuteSimulation()
# 13) 数据提取和可视化
analyze_and_plot_results(locLog, trackLog, navAttLog, navTransLog, rwSpeedLog,
mrpTorqueLog, accessLog, groundStateLog, numRW)
print(f"Ground pointing simulation completed, simulation time: {sim_hours} hours")
def analyze_and_plot_results(locLog, trackLog, navAttLog, navTransLog, rwSpeedLog,
mrpTorqueLog, accessLog, groundStateLog, numRW):
"""
分析和可视化仿真结果
"""
# 设置英文字体 - Times New Roman
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['font.size'] = 12
plt.rcParams['axes.unicode_minus'] = False
# 提取数据
sigma_BR = trackLog.sigma_BR # MRP误差
omega_BR_B = trackLog.omega_BR_B # 角速度误差
wheelSpeeds = rwSpeedLog.wheelSpeeds[:, :numRW] # 反作用轮转速
cmdTorque = mrpTorqueLog.torqueRequestBody # 控制力矩
hasAccess = accessLog.hasAccess # 地面站可见性
r_BN_N = navTransLog.r_BN_N # 航天器位置
# 时间轴
t_track_min = trackLog.times() * mc.NANO2MIN
t_rw_min = rwSpeedLog.times() * mc.NANO2MIN
t_access_min = accessLog.times() * mc.NANO2MIN
t_pos_min = navTransLog.times() * mc.NANO2MIN
# === Figure 1: Attitude Control Performance ===
plt.figure(figsize=(12, 6))
# MRP attitude error
plt.subplot(2, 1, 1)
sigma_arr = np.asarray(sigma_BR)
mrp_norm = np.linalg.norm(sigma_arr, axis=1)
phi_err_deg = 4.0 * np.degrees(np.arctan(mrp_norm)) # Principal angle error
plt.plot(t_track_min, phi_err_deg, 'b-', linewidth=2)
plt.axhline(1.0, color='r', linestyle='--', alpha=0.7, label='1° threshold')
plt.ylabel('Pointing Error (degrees)')
plt.title('Ground Station Pointing Control Performance')
plt.grid(True)
plt.legend(loc='lower right', frameon=True, facecolor='white', edgecolor='gray',
framealpha=0.9, fontsize=8)
# Ground station access
plt.subplot(2, 1, 2)
access_arr = np.asarray(hasAccess).flatten()
plt.plot(t_access_min, access_arr, 'k-', linewidth=2)
plt.ylabel('Ground Station Access')
plt.xlabel('Time (minutes)')
plt.ylim([-0.05, 1.05])
plt.grid(True)
plt.tight_layout()
plt.show()
# === Figure 2: Reaction Wheel Status ===
plt.figure(figsize=(12, 6))
# Reaction wheel speeds
plt.subplot(2, 1, 1)
wheelSpeeds_rpm = wheelSpeeds * 60.0 / (2*np.pi) # Convert to RPM
for i in range(numRW):
plt.plot(t_rw_min, wheelSpeeds_rpm[:, i], label=f'RW{i+1}')
plt.ylabel('Reaction Wheel Speed (RPM)')
plt.title('Reaction Wheel Status Monitoring')
plt.grid(True)
plt.legend(loc='lower right', frameon=True, facecolor='white', edgecolor='gray',
framealpha=0.9, fontsize=8)
# Control torques
plt.subplot(2, 1, 2)
torque_arr = np.asarray(cmdTorque)
plt.plot(t_rw_min, torque_arr[:, 0], 'r-', label='Tx')
plt.plot(t_rw_min, torque_arr[:, 1], 'g-', label='Ty')
plt.plot(t_rw_min, torque_arr[:, 2], 'b-', label='Tz')
plt.ylabel('Control Torque (N·m)')
plt.xlabel('Time (minutes)')
plt.grid(True)
plt.legend(loc='lower right', frameon=True, facecolor='white', edgecolor='gray',
framealpha=0.9, fontsize=8)
plt.tight_layout()
plt.show()
# === Figure 3: Orbital Position ===
plt.figure(figsize=(12, 6))
# Position components
pos_arr = np.asarray(r_BN_N) / 1000.0 # Convert to km
for i in range(3):
plt.plot(t_pos_min, pos_arr[:, i], label=f'r_{["x","y","z"][i]} (km)')
plt.ylabel('Position (km)')
plt.xlabel('Time (minutes)')
plt.title('Spacecraft Orbital Position')
plt.grid(True)
plt.legend(loc='lower right', frameon=True, facecolor='white', edgecolor='gray',
framealpha=0.9, fontsize=8)
plt.tight_layout()
plt.show()
# === Performance Statistics ===
final_error = phi_err_deg[-1]
avg_error = np.mean(phi_err_deg)
max_torque = np.max(np.abs(torque_arr))
access_ratio = np.mean(access_arr) * 100
print(f"\n=== Ground Pointing Performance Statistics ===")
print(f"Final pointing error: {final_error:.3f}°")
print(f"Average pointing error: {avg_error:.3f}°")
print(f"Maximum control torque: {max_torque:.4f} N·m")
print(f"Ground station access ratio: {access_ratio:.1f}%")
# Calculate alignment ratio (< 1 degree considered good alignment)
aligned = phi_err_deg < 1.0
align_ratio = np.mean(aligned) * 100
print(f"Good alignment time ratio: {align_ratio:.1f}% (error < 1°)")
# Performance during access periods
in_access = access_arr > 0.5
if np.any(in_access):
access_errors = phi_err_deg[in_access[:len(phi_err_deg)]]
print(f"Average error during access: {np.mean(access_errors):.3f}°")
if __name__ == "__main__":
print("Starting simplified ground pointing simulation...")
run_ground_pointing(sim_hours=6) # Simulate for 1.5 hours, including several orbital periods