算法前缀和


【算法】前缀和
一维前缀和
1、算法作用
快速求出数组中某个连续区间的和。
2、算法原理
第一步:根据待求和数组,预先创建一个前缀和数组,前缀和数组的第 i 个元素是待求和数组的下标为 1 到 i 闭区间所有元素的和。
比如 int arr[ ] = { 1,4,7,2,5,8,3,6,9 },那么前缀和数组 int dp[ ] = { 1,5,12,14,19,27,30,36,45 }。
前缀和数组满足:dp[i] = dp[i - 1] + arr[i]。
第二步:对于 arr 数组以 l 和 r 为下标的闭区间,其中元素的总和为:dp[r] - dp[l - 1].
3、细节处理
上面在求和时,出现了 dp[l - 1],所以 l 是 >= 1 的,即:把 arr 数组的下标看成是从 1 开始的,前缀和数组的首元素默认是 0。
4、时间复杂度
如果求和的次数是 q 次,那么时间复杂度是 O(q) + O(N)。
二维前缀和
1、算法作用
快速计算出一个矩阵中任意一个子矩阵的元素的和
2、算法原理
第一步:根据待求和矩阵,预先创建一个前缀和矩阵,前缀和矩阵的元素 dp[i][j] 表示待求和矩阵从[1][1] 到 [i][j] 子矩阵的所有元素的和。
在创建前缀和矩阵时,如果每次都从[1][1]开始遍历求和,效率就会下降。
如果待求和矩阵为 arr,前缀和矩阵为 dp 那么:
前缀和矩阵满足: dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1]
解释:
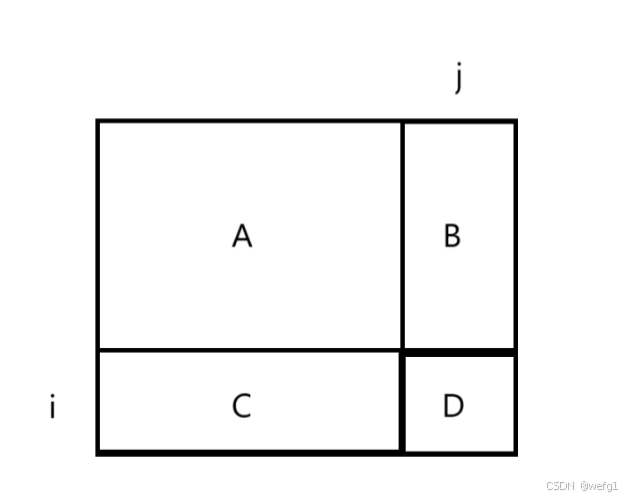
dp[i][j] = A + B + C + D,但是 C 和 B 部分的和不好求,而在求 D 之前 ,A + B 部分的和以及 A + C 部分的和应该是已知的,所以 dp[i][j] = AB + AC - A + D。
第二步:前缀和矩阵创建好了,那我们该如何使用它呢?如果子矩阵是以左上角的坐标(x1,y1)和右下角(x2,y2)的坐标表示的,那么该子矩阵内的元素的和为:
dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]
解释:
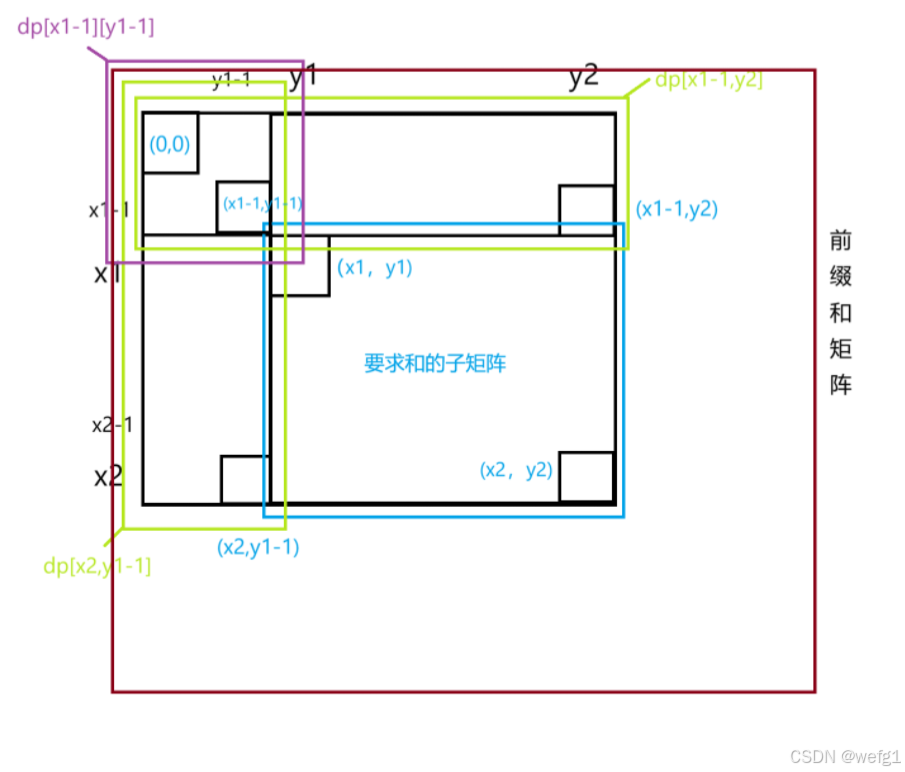
蓝色部分是要求和的部分,它的和等于 dp[x2][y2] 减去两个绿色部分面积再加上紫色部分面积。
3、细节处理
以上出现的式子出现了 i - 1,j - 1,x1 - 1 等,说明 i、j 等都是大于等于 1 的数,也就是说前缀和矩阵的横纵坐标都是从 1 开始的,前缀和矩阵的第一排和第一列的元素都是 0.
4、时间复杂度
创建前缀和矩阵时遍历了一遍待求和矩阵,如果求和次数是 q 次,时间复杂度为 O(N) +O(q).
例题

#include <iostream>
#include <vector>
using namespace std;
int main() {
// 读取数据
int n,q;
cin >> n >> q;
vector<long long> arr(n + 1);
for(int i = 1; i <= n; i++) cin >> arr[i];
// 创建前缀和数组
vector<long long> dp(n + 1);
for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];
// 使用前缀和数组
int l = 0,r = 0;
while(q--)
{
cin >> l >> r;
cout << (dp[r] - dp[l - 1]) << endl;
}
}
#include <iostream>
#include <vector>
using namespace std;
int main() {
// 读入数据
int n = 0,m = 0,q = 0;
cin >> n >> m >> q;
vector<vector<int>> arr(n + 1,vector<int>(m + 1));
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> arr[i][j];
}
}
// 创建前缀和矩阵
vector<vector<long long>> dp(n + 1,vector<long long>(m + 1));
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
}
}
//使用前缀和矩阵
int x1 = 0,y1 = 0,x2 = 0,y2 = 0;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2;
cout << (dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]) << endl;
}
return 0;
}
解析:不能死记硬背,前缀和数组的第 i 个元素不仅可以表示原数组[ 0,i ] 所有元素的和,还可以表示原数组[ 0,i ] 所有元素的最大值、平均值、众数、方差等等,这道题可以表示原数组[ 0,i - 1] 所有元素的和。同时,还可以创建一个后缀和数组,它的第 i 个元素表示原数组[ i + 1,n - 1 ] 所有元素的和,其中 n 是原数组的元素个数,后缀和数组的填表顺序是从后往前.
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n = nums.size();
//创建前缀和数组和后缀和数组
vector<int> f(n),g(n);
for(int i = 1; i < n; i++) f[i] = f[i - 1] + nums[i - 1];
for(int i = n - 2; i >= 0; i--) g[i] = g[i + 1] + nums[i + 1];
for(int i = 0; i < nums.size(); i++) if(f[i] == g[i]) return i;
return -1;
}
};
解析:这道题的解题思想与上一道题差不多。预先创建一个前缀和数组和后缀和数组,前缀和数组第 i 个元素表示原数组[ 0,i - 1] 所有元素的积,后缀和数组表示原数组[ i + 1,n - 1] 所有元素的积。最终要返回的数组的第 i 个元素 = f[i] * g[i] 。
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> f(n , 1); // 前缀和数组
vector<int> g(n , 1); // 后缀和数组
for(int i = 1; i < n; i++) f[i] = f[i - 1] * nums[i - 1];
for(int i = n - 2; i >= 0; i--) g[i] = g[i + 1] * nums[i + 1];
vector<int> ret(n);
for(int i = 0; i < n; i++) ret[i] = f[i] * g[i];
return ret;
}
};
解析:前缀和 + 哈希表。将 i 位置之前的所有前缀和放到哈希表里,看看哈希表里有多少前缀和等于 sum - k(sum 是 i 位置的前缀和)。hash<int,int> :第一个 int:前缀和,第二个 int:个数。假设 i 位置之前的前缀和(不包括 i 位置)为 sum - k 的位置有 m 个,说明从这些位置到 i 位置(包括 i 位置)的元素总和就是 k。
细节问题:
1、前缀和进入哈希表的时机:应该在寻找前缀和为 sum - k 的位置之后。
2、如果 [0,i - 1] 元素的总和恰好为 k,此时 sum - k=0,所以哈希表在初始化时应该让 hash[0] = 1
3、不用真的创建一个前缀和数组,只需用 sum 变量记录 i 位置的前缀和,将sum放入哈希表即可
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0] = 1;
int sum = 0,ret = 0;
for(auto x : nums)
{
sum += x;
if(hash.count(sum - k)) ret += hash[sum - k];
hash[sum]++;
}
return ret;
}
};下一道题的大概思路与这道题相同,但在做下一道题之前需要掌握:
同余定理
如果 a - b 可以被 p 整除,那么 a % p = b % p。反之亦成立。
负数模正数的结果和修正
在 C++ 或 java 中,一个负数模上一个正数的结果是负数,正数模上正数的结果是正数。现在修正为不管是正数还是负数模上正数的结果都是正数:(a%p + p)% p ,即 (a%p + p)% p 等于 a%p 的绝对值。

解析:前缀和 + 哈希表。具体步骤如下:
- 将 i 位置之前的所有前缀和存储到哈希表中
- 计算当前前缀和sum对k取模的结果
- 根据同余定理,(sum - x) % k == 0 等价于 sum % k == x % k
- 因此只需要统计哈希表中与当前sum同余的前缀和个数
- 由于sum可能为负数,需要对sum % k的结果进行修正:(sum % k + k) % k
- 哈希表中存储的是修正后的取模结果,而非原始前缀和
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0] = 1;
int ret = 0,sum = 0;
for(auto i : nums)
{
sum += i;
int r = (sum % k + k) % k;
if(hash.count(r)) ret += hash[r];
hash[r]++;
}
return ret;
}
};