LeetCode热题-100238.-除自身以外数组的乘积

目录

LeetCode热题 100——238. 除自身以外数组的乘积
题目:
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 **不要使用除法,**且在
O(n)时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
图文解析:
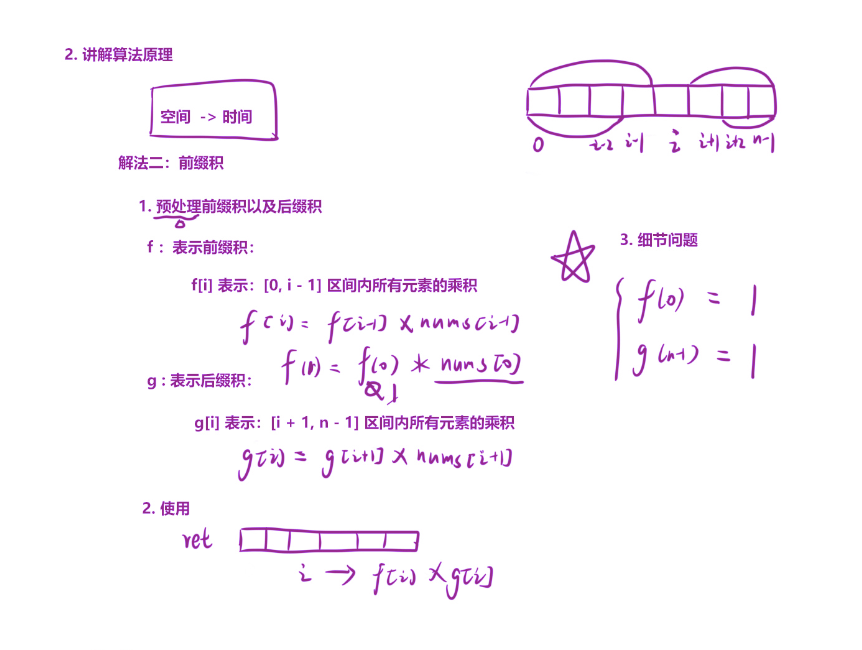
核心思想:分治思想
将问题分解为两个部分:
- 左边所有元素的乘积(前缀积)
- 右边所有元素的乘积(后缀积)
最终结果 = 左边乘积 × 右边乘积
为什么这样设计?
- 直接计算每个位置的乘积需要O(n²)时间
- 使用前缀和后缀数组可以将时间复杂度降为O(n)
- 避免了重复计算,提高了效率
📊 示例演示
假设 nums = [1, 2, 3, 4]
步骤1:计算前缀积数组 l
i=0: l[0] = 1
i=1: l[1] = l[0] × nums[0] = 1 × 1 = 1
i=2: l[2] = l[1] × nums[1] = 1 × 2 = 2
i=3: l[3] = l[2] × nums[2] = 2 × 3 = 6
l = [1, 1, 2, 6]步骤2:计算后缀积数组 r
i=3: r[3] = 1
i=2: r[2] = r[3] × nums[3] = 1 × 4 = 4
i=1: r[1] = r[2] × nums[2] = 4 × 3 = 12
i=0: r[0] = r[1] × nums[1] = 12 × 2 = 24
r = [24, 12, 4, 1]步骤3:合并结果
ret[0] = l[0] × r[0] = 1 × 24 = 24
ret[1] = l[1] × r[1] = 1 × 12 = 12
ret[2] = l[2] × r[2] = 2 × 4 = 8
ret[3] = l[3] × r[3] = 6 × 1 = 6
ret = [24, 12, 8, 6]验证:确实 1×2×3×4=24,去掉每个位置自身后得到正确结果。
代码实现:
class Solution {
/**
* 计算数组中每个元素除自身外其他元素的乘积
* 时间复杂度:O(n),空间复杂度:O(n)(输出数组不计入空间复杂度时为O(1))
*
* @param nums 输入数组
* @return 结果数组,其中ret[i] = nums[0] × nums[1] × ... × nums[i-1] × nums[i+1] × ... × nums[n-1]
*/
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
// 前缀积数组:l[i] 表示nums[0]到nums[i-1]的乘积
// l[0] = 1 (因为0前面没有元素)
// l[1] = nums[0]
// l[2] = nums[0] × nums[1]
// ...
// l[i] = nums[0] × nums[1] × ... × nums[i-1]
int[] l = new int[n];
// 后缀积数组:r[i] 表示nums[i+1]到nums[n-1]的乘积
// r[n-1] = 1 (因为n-1后面没有元素)
// r[n-2] = nums[n-1]
// r[n-3] = nums[n-2] × nums[n-1]
// ...
// r[i] = nums[i+1] × nums[i+2] × ... × nums[n-1]
int[] r = new int[n];
// 初始化边界值
l[0] = 1; // 第一个元素的前缀积为1(空乘积)
r[n - 1] = 1; // 最后一个元素的后缀积为1(空乘积)
// 计算前缀积:从左到右遍历
// 对于每个位置i,l[i] = l[i-1] × nums[i-1]
for (int i = 1; i < n; i++) {
l[i] = l[i - 1] * nums[i - 1];
}
// 计算后缀积:从右到左遍历
// 对于每个位置i,r[i] = r[i+1] × nums[i+1]
for (int i = n - 2; i >= 0; i--) {
r[i] = r[i + 1] * nums[i + 1];
}
// 创建结果数组
int[] ret = new int[n];
// 合并前缀积和后缀积得到最终结果
// ret[i] = l[i] × r[i] = (前缀积) × (后缀积)
// = (nums[0]×...×nums[i-1]) × (nums[i+1]×...×nums[n-1])
for (int i = 0; i < n; i++) {
ret[i] = l[i] * r[i];
}
return ret;
}
}