数据挖掘-6.1-其他降维方法不是很重要


数据挖掘 6.1 其他降维方法(不是很重要)
6.1 Other dimensionality reduction methods
6.1 其他降维方法
前言
问题
降维与相关性的哲学问题
核心问题
为什么我们实际上能够降维?
不同事物之间的相关性从何而来?
不仅仅是 PCA
不只是 PCA,还有其他机器学习方法也依赖相关性。
如果数据完全是随机的、没有结构,那么所有相关性都不存在,我们就无法降维。
举例说明
即使两个样本在外观或训练测试上差异很大,看起来非常不同,但它们可能仍然遵循同样的潜在规则。
结论
降维方法依赖于数据中的潜在相关性。
问题在于:这种潜在相关性到底从何而来?
类似的问题:为什么一个人的身高和体重之间会有关联?
答案
数据中存在结构
在所谓“流形”的东西上,流形本身就是一种结构。
数据不是完全随机的,而是有某种潜在结构。
PCA 的作用
PCA 能发现这种结构,尽管它假设的是线性关系,但现实中并不总是线性的。
因此,除了 PCA,我们还需要学习其他方法来处理这种“流形结构”。
核心问题
这些相关性(数据结构、流形)从何而来?
为什么我们能通过数据去推断出维度?
答案
因为背后有物理约束。
数据的产生过程不是完全自由或随机的,而是受到物理规律、自然法则的限制。如果数据真的完全是随机的,就不会呈现出任何结构,也就谈不上降维或发现相关性。
流形
数据所在的结构称为流形。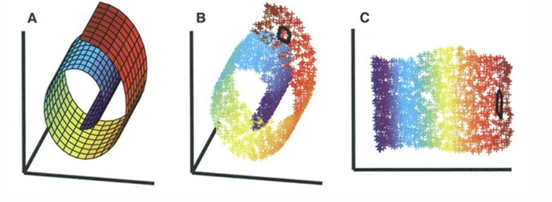
3 降维大纲
在真实数据集中,许多变量可能是相关的。因此,数据集的有效维度可能比特征数目更低。所以,数据实际上存在于某个 流形(manifold) 上。
降维方法
3.1 线性方法
PCA(主成分分析)
LDA(线性判别分析)
CCA :Canonical Component Analysis 典型相关分析
3.2 非线性方法
3.2.1 流形学习方法(Manifold Learning)
目标:揭示隐藏在高维数据中的低维结构
Kernel PCA(核主成分分析)
MDS(多维尺度分析)
LLE(局部线性嵌入)
t-SNE
3.2.2 概率方法(Probabilistic Approaches)
ICA(独立成分分析)
3.2.3 拓扑数据分析(Topological Data Analysis)
目标:保持数据的拓扑结构
方法:UMAP
3.3 监督降维方法
结合监督学习的降维技术
不相关与独立

核化PCA(Kernelized PCA)
在下图的情况中,在上面应用PCA,不会能找到最大方差的任何方向,因为所有方向都差不多。
PCA 与核化PCA
区别在于把 协方差矩阵 C C C 换成了核函数 f ( x ) f(x) f(x)。
PCA(主成分分析)
假设数据结构是 线性 的,通过协方差矩阵分解找到最大方差方向。
协方差矩阵:
C
1 N ∑ i
1
N
(
x
i
−
x
ˉ
)
(
x
i
−
x
ˉ
)
T
C = \frac{1}{N} \sum_{i=1}^N (x_i - \bar{x})(x_i - \bar{x})^T
C=N1i=1∑N(xi−xˉ)(xi−xˉ)T
优化目标:
max w w T C w s u b j e c t w T w
1 \max_w \ w^T C w \ subject \quad w^T w = 1 wmax wTCwsubjectwTw=1
核化PCA(Kernel PCA)
使用核函数将数据隐式映射到高维特征空间,在高维空间中做线性PCA,从而实现 非线性降维。
核矩阵:
K i j
k ( x i , x j ) K_{ij} = k(x_i, x_j) Kij=k(xi,xj)
优化目标:
max α α T K α s u b j e c t α T α
1 \max_\alpha \ \alpha^T K \alpha \ subject \quad \alpha^T \alpha = 1 αmax αTKαsubjectαTα=1
